Combinatorics
Welcome to Our Site
I greet you this day,
These are the solutions to the Cambridge O-Level (Ordinary Level) past questions on Combinatorics.
The link to the video solutions will be provided for you. Please subscribe to the YouTube channel to be notified
of upcoming livestreams.
You are welcome to ask questions during the video livestreams.
If you find these resources valuable and if any of these resources were helpful in your passing the
any of the Cambridge Assessments on Mathematics, please consider making a donation:
Cash App: $ExamsSuccess or
cash.app/ExamsSuccess
PayPal: @ExamsSuccess or
PayPal.me/ExamsSuccess
Google charges me for the hosting of this website and my other
educational websites. It does not host any of the websites for free.
Besides, I spend a lot of time to type the questions and the solutions well.
As you probably know, I provide clear explanations on the solutions.
Your donation is appreciated.
Comments, ideas, areas of improvement, questions, and constructive criticisms are welcome.
Feel free to contact me. Please be positive in your message.
I wish you the best.
Thank you.
Formula Sheet: List of Formulae
Formulas
Say:
n is the number of items (n items)
c and d are the number of duplicate items
n! is read as n-factorial
The number of permutations of nitems is n!
The number of permutations of duplicate items is $\dfrac{n!}{c! * d!}$
The number of permutations of $n$ total items taking $r$ items at a time is $^nP_r \;\;\;or\;\;\; _nP_r
\;\;\;or\;\;\; P(n, r)$
The number of combinations of $n$ total items taking $r$ items at a time is $^nC_r \;\;\;or\;\;\; _nC_r
\;\;\;or\;\;\; C(n, r) \;\;\;or\;\;\; \displaystyle{\binom{n}{r}}$
$
(1.)\:\: 0! = 1 \\[4ex]
(2.)\:\: n! = n * (n - 1) * (n - 2) * (n - 3) * ... * 1 \\[4ex]
(3.)\;\; n! = n * (n - 1)! \\[4ex]
(4.)\;\; n! = n * (n - 1) * (n - 2)!...\text{and so on and so forth} \\[4ex]
(5.)\;\; (n - 1)! = (n - 1) * (n - 2)!...\text{and so on and so forth} \\[4ex]
(6.)\;\; (n - 2)! = (n - 2) * (n - 3) * (n - 4)!...\text{and so on and so forth} \\[4ex]
(7.)\;\; (n - 3)! = (n - 3) * (n - 4) * (n - 5)!...\text{and so on and so forth} \\[4ex]
(8.)\;\; (n + 1)! = (n + 1) * n!...\text{and so on and so forth} \\[4ex]
(9.)\;\; (n + 2)! = (n + 2) * (n + 1) * n!...\text{and so on and so forth} \\[4ex]
(10.)\;\; (n + 3)! = (n + 3) * (n + 2) * (n + 1) * n!...\text{and so on and so forth} \\[4ex]
(11.)\:\: P(n, r) = \dfrac{n!}{(n - r)!} \\[7ex]
(12.)\:\: C(n, r) = \dfrac{n!}{(n - r)!r!} \\[7ex]
(13.)\;\; P(n, r) = n! * C(n, r) \\[4ex]
(14.)\;\; C(n, r) = C(n, n - r) \\[4ex]
(15.)\;\; (n - r) * P(n, r) = P(n, r + 1) \\[4ex]
(16.)\;\; Number\;\;of\;\;circular\;\;permutations = (n - 1)! \\[4ex]
$
Case 1:
Given: a certain number of digits/letters say p
(14.) The number of unique number of digits/letters say c digits/letters that can be formed if the
digits/letters may be repeated is $p^c$ digits/letters.
(15.) The number of unique number of digits/letters say c digits/letters that can be formed if the
digits/letters may not be repeated is $P(p, c)$ digits/letters.
Case 2:
Given: a certain number of people or items in a linear random order say $n$
(16.) The number of ways in which two people or two items must be close together is $2 * (n - 1) * (n - 2)!$
ways
Binomial Theorem
$
(x + y)^n \\[3ex]
= C(n, 0)(x^n)(y^0) + C(n, 1)(x^{n - 1})(y) + C(n, 2)(x^{n - 2})(y^2) + ... + C(n, r)(x^{n - r})(y^r) + ... +
C(n, n)(x^0)(y^n) \\[4ex]
= x^n + C(n, 1)(x^{n - 1})(y) + C(n, 2)(x^{n - 2})(y^2) + ... + C(n, r)(x^{n - r})(y^r) + ... + y^n \\[5ex]
$
Generalized Binomial Series
Recommended for negative values of the outside exponent (negative values of n)
$
(1 + x)^n = 1 + nx + \dfrac{n(n - 1)}{2!}x^2 + \dfrac{n(n - 1)(n - 2)}{3!}x^3 + O(x^4) \\[3ex]
$
where $O(x^4)$ is the Big-O Notation representing the remainder of the series, and indicating that the omitted
terms are of the order of $x^4$ as x approaches zero.
The binomial expansion of $(1 + ax)^n$ is valid when $|ax| \lt 1$
(a.) the O and A are not next to each other
(b.) the letters MATHS are together in this order.
Number of different arrangements of the 9 letters of POLYMATHS = 9!
(a.) Event: O and A must not be together
Complementary Event: O and A must be together.
To solve this question, it is better to assume that O and A must be together.
Let us begin with the complementary event.
We shall consider two arrangements:
1st: Assume O and A must be together: the two letters are treated as a single unit
Type: Permutation
Hence, we have: (7 + 1)! = 8! arrangements
2nd: Within the single unit of O and A, the two letters can be arranged in 2! ways
It can be OA or AO
Hence, we have 2! arrangements
The total number of arrangements if O and A must be together = 8! * 2!
The number of different arrangements if O and A are not together is:
Number of different arrangements of the 9 letters − Number of arrangements if O and A must be together
= 9! − (2! * 8!)
= 282240 arrangements
(b.) If the letters MATHS must be together in this order
MATHS is treated as a single unit in that order.
So, we have POLY + (MATHS)
Hence, the number of arrangements
= (4 + 1)!
= 5!
= 120 arrangements.
Find the values of the constants n, a and b.
$ \underline{\text{First thre terms of the expansion in increasing powers of }} x \\[3ex] \left(2 + \dfrac{x}{2}\right)^n \\[5ex] = 2^n + C(n, 1)(2^{n - 1})\left(\dfrac{x}{2}\right)^1 + C(n, 2)(2^{n - 2})\left(\dfrac{x}{2}\right)^2 \\[5ex] = 2^n + \dfrac{n!}{(n - 1)! * 1!}(2^{n - 1})\left(\dfrac{x}{2}\right) + \dfrac{n!}{(n - 2)! * 2!}(2^{n - 2})\left(\dfrac{x^2}{4}\right) \\[5ex] = 2^n + \dfrac{n (n - 1)!}{(n - 1)!} * 2^{n - 1} * \dfrac{x}{2} + \dfrac{n(n - 1)(n - 2)!}{(n - 2)! * 2} * 2^{n - 2} * \dfrac{x^2}{4} \\[5ex] = 2^n + n * 2^{n - 1} * \dfrac{x}{2} + \dfrac{n(n - 1)}{2} * 2^{n - 2} * \dfrac{x^2}{4} \\[5ex] = b + abx + \dfrac{9}{8}abx^2 \\[5ex] \underline{\text{Compare and Equate terms}} \\[3ex] b = 2^n ...eqn.(1) \\[3ex] abx = n * 2^{n - 1} * \dfrac{x}{2} \\[5ex] ab = n * 2^{n - 1} * \dfrac{1}{2} \\[5ex] \text{Substitute for b from eqn.(1)} \\[3ex] a * 2^n = n * \dfrac{2^{n - 1}}{2^1} \\[5ex] a = \dfrac{n * 2^{n - 1}}{2^n * 2^1} \\[5ex] a = \dfrac{n * 2^{n - 1}}{2^{n + 1}} \\[5ex] a = n * 2^{n - 1 - (n + 1)} \\[4ex] a = n * 2^{n - 1 - n - 1} \\[5ex] a = n * 2^{-2} \\[4ex] a = n * \dfrac{1}{2^2} \\[5ex] a = \dfrac{n}{4} ...eqn.(2) \\[5ex] \dfrac{9}{8}abx^2 = n(n - 1) * 2^{n - 2} * \dfrac{x^2}{4} \\[5ex] \text{Substitute for a and b from eqn.(1) and eqn.(2)} \\[3ex] \dfrac{9}{8} * \dfrac{n}{4} * 2^n * x^2 = \dfrac{n(n - 1)}{2} * 2^{n - 2} * \dfrac{x^2}{4} \\[5ex] 9 * \dfrac{1}{4} * 2^n = (n - 1) * 2^{n - 2} \\[5ex] n - 1 = 9 * \dfrac{1}{4} * 2^n * \dfrac{1}{2^{n - 2}} \\[5ex] n - 1 = \dfrac{9}{4} * \dfrac{2^n}{2^{n - 2}} \\[5ex] n - 1 = \dfrac{9}{4} * 2^{n - (n - 2)} \\[5ex] n - 1 = \dfrac{9}{4} * 2^{n - n + 2} \\[5ex] n - 1 = \dfrac{9}{4} * 2^2 \\[5ex] n - 1 = \dfrac{9}{4} * 4 \\[5ex] n = 9 + 1 \\[3ex] n = 10 \\[5ex] \text{Substitute for n in eqn.(2)} \\[3ex] a = \dfrac{10}{4} \\[5ex] a = \dfrac{5}{2} \\[5ex] \text{Substitute for n in eqn.(1)} \\[3ex] b = 2^{10} \\[3ex] b = 1024 $
(a.) The choir stands in a single straight line.
(i.) Find the number of possible arrangements if the first person and last person are both women.
(ii.) Find the number of possible arrangements if all the children stand next to each other.
(b.) Four of the choir are selected to sing in a group.
(i.) Find the number of different selections if no man is chosen.
(ii.) Find the number of different selections if at least 2 women are selected.
3 women + 2 men + 4 children = 9 people
(a.) (i.) Arranging 9 people in a single straight line
Condition: The first person and the last person in the line are women
1st: Any of the 3 women can stand as the first person in the line.
Number of arrangements = 3
2nd: Any of the remaining two women can stand as the last person in the line.
Number of arrangements = 2
The remaining 7 people (9 − 2 = 7) can be arranged in 7! ways
Number of arrangements = 7!
Total number of possible arrangements
= 3 * 2 * 7!
= 30240 arrangements.
(ii.) If the 4 children must stand next to each other:
Type: Permutation
1st: They are treated as a single unit
Number of arrangements = (3 + 2 + 1)! = 6!
2nd: Within the block of the 4 children, they can be arranged in 4! ways among themselves
Number of arrangements = 4!
Total number of possible arrangements
= 6! * 4!
= 17280 arrangements.
(b.) Selecting 4 from the choir of 9 people: This is Combination because the order of selection does not matter.
(i.) Condition: No man must be in the four people selected
There are 2 men
This leaves us with: 9 people − 2 men = 7 people
So, we have to select 4 people from 7 people
$ \text{Number of selections} \\[3ex] = C(4, 7) \\[3ex] = \dfrac{7!}{(7 - 4)! * 4!} \\[5ex] = 35\text{ selections} \\[3ex] $ (ii.) Condition: At least 2 women must be selected
Type: Combination
There are 3 women
At least 2 means 2 or more
At least 2 women in the context of the question = 2 women or 3 women
1st: Select 2 women from 3 women and the remaining 2 people (4 − 2) from 6 people (9 − 3)
OR
Select 3 women from 3 women and the remaining 1 person (4 − 3) from 6 people (9 − 3)
$ \text{Number of selections} \\[3ex] = C(3, 2) * C(6, 2) \hspace{3em}OR\hspace{3em} C(3, 3) * C(6, 1) \\[3ex] = \left[\dfrac{3!}{(3 - 2)! * 2!} * \dfrac{6!}{(6 - 2)! * 2!}\right] + \left[\dfrac{3!}{(3 - 3)! * 3!} * \dfrac{6!}{(6 - 1)! * 1!}\right] \\[5ex] = (3 * 15) + (1 * 6) \\[3ex] = 45 + 6 \\[3ex] = 51\text{ selections} $
Find the value of x.
(b.) In the expansion of $\left(x + \dfrac{2}{x}\right)^n$ in decreasing powers of x, the 6th term is a constant.
(i.) Find the value of the positive integer n.
(ii.) Find the value of the 6th term.
$ (a.) \\[3ex] \text{Expansion of }(x + x^2)^8 \text{ in ascending powers of } x \\[3ex] \text{3rd term} = C(8, 2) * x^6 * (x^2)^2 \\[3ex] = \dfrac{8!}{(8 - 2)! * 2!} * x^6 * x^4 \\[5ex] = 28 * x^{6 + 4} \\[3ex] = 28x^{10} \\[5ex] \text{6th term} = C(8, 5) * x^3 * (x^2)^5 \\[3ex] = \dfrac{8!}{(8 - 5)! * 5!} * x^3 * x^{10} \\[5ex] = 56 * x^{3 + 10} \\[3ex] = 56x^{13} \\[5ex] \text{3rd term} = \text{6th term} \\[3ex] \implies \\[3ex] 28x^{10} = 56x^{13} \\[3ex] \dfrac{x^{13}}{x^{10}} = \dfrac{28}{56} \\[5ex] x^{13 - 10} = \dfrac{1}{2} \\[5ex] x^3 = \dfrac{1}{2} \\[5ex] x = \sqrt[3]{\dfrac{1}{2}} \\[5ex] x = \dfrac{\sqrt[3]{1}}{\sqrt[3]{2}} \\[5ex] x = \dfrac{1}{\sqrt[3]{2}} * \dfrac{\sqrt[3]{4}}{\sqrt[3]{4}} \\[5ex] x = \dfrac{\sqrt[3]{4}}{\sqrt[3]{8}} \\[5ex] x = \dfrac{\sqrt[3]{4}}{2} \\[5ex] (b.) \\[3ex] \text{Expansion of }\left(x + \dfrac{2}{x}\right)^n \text{ in decreasing powers of } x \\[5ex] \text{6th term} = C(n, 5) * x^{n - 5} * \left(\dfrac{2}{x}\right)^5 \\[5ex] = \dfrac{n!}{(n - 5)! * 5!} * x^{n - 5} * \dfrac{32}{x^5} \\[5ex] = \dfrac{n!}{(n - 5)! * 5!} * \dfrac{x^n}{x^5} * \dfrac{32}{x^5} \\[5ex] = \dfrac{n!}{(n - 5)! * 5!} * \dfrac{x^n}{x^5 * x^5} * 32 \\[5ex] = \dfrac{n!}{(n - 5)! * 5!} * \dfrac{x^n}{x^{5 + ^5}} * 32 \\[5ex] = \dfrac{n!}{(n - 5)! * 5!} * \dfrac{x^n}{x^{10}} * 32 \\[5ex] = \dfrac{n!}{(n - 5)! * 5!} * x^{n - 10} * 32 \\[5ex] $ For the 6th term to be a constant, that means that the variable, x should be 1
The variable should not be zero because it will make the entire 6th term to be 0
The variable should be 1
For the variable, x to be 1, the index/power/exponent must be zero
Anything raised to exponent zero gives 1...Law 3...Exp
So, this implies that:
$ (i.) \\[3ex] x^{n - 10} = 1 \\[3ex] x^{n - 10} = x^0 \\[3ex] \text{same base; equate exponents} \\[3ex] n - 10 = 0 \\[3ex] n = 10 \\[5ex] (ii.) \\[3ex] \text{6th term} = \dfrac{10!}{(10 - 5)! * 5!} * x^{10 - 10} * 32 \\[5ex] = 252 * 1 * 32 \\[5ex] = 8064 $
Find the number of possible orders in each of the following cases.
(i.) No girls are next to each other.
(ii.) The 2 boys are not next to each other.
(b.) 12 people, including Anjie and Bubay, are divided into 3 groups of 4 people.
Anjie and Bubay must not be in the same group.
Find the number of ways in which the 3 groups can be selected.
(a.) In this case, the number of girls is more than the number of boys.
So, we shall use the Gaps (Spacing) method this time.
$ (i.) \\[3ex] \text{3 girls and 2 boys} \\[3ex] \text{No girls are next to each other} \\[3ex] \underline{\text{1st Case}}: \\[3ex] \begin{array}{c c c c c} \stackrel{\Large G}{\rule{1cm}{0.5mm}} & \stackrel{\Large B}{\rule{1cm}{0.5mm}} & \stackrel{\Large G}{\rule{1cm}{0.5mm}} & \stackrel{\Large B}{\rule{1cm}{0.5mm}} & \stackrel{\Large G}{\rule{1cm}{0.5mm}} \end{array} \\ \begin{array}{c c c c c} \stackrel{\Large 3}{\rule{1cm}{0.5mm}} & \stackrel{\Large 2}{\rule{1cm}{0.5mm}} & \stackrel{\Large 2}{\rule{1cm}{0.5mm}} & \stackrel{\Large 1}{\rule{1cm}{0.5mm}} & \stackrel{\Large 1}{\rule{1cm}{0.5mm}} \end{array} $
This is the only case that works.
Any of the 3 girls can take the first position: 3 ways
Any of the 2 boys can take the second position: 2 ways
Any of the remaining 2 girls (3 − 1) can take the third position: 2 ways
The remaining boy must take the fourth position: 1 way
The remaining girl must take the fifth position: 1 way
Number of possible orders
= 3 * 2 * 2 * 1 * 1
= 12 arrangements.
Type: Permutation
Case 1: No restriction
3 girls and 2 boys = 5 people
Number of arrangements = 5!
Case 2: Condition: Assume the 2 boys are next to each other.
Type: Permutation
1st: They are treated as a single unit
Number of arrangements = (3 + 1)! = 4!
2nd: Within the block of the 2 boys, they can be arranged in 2! ways between each other
Number of arrangements = 2!
Total number of possible arrangements if the 2 boys are next to each other
= 4! * 2!
(ii.) Case 3: Condition: The 2 boys are not next to each other.
Number of arrangements
= Case 1 − Case 2
= 5! − (4! * 2!)
= 72 possible orders.
(b.) 12 people, including Anjie and Bubay, are divided into 3 groups of 4 people.
Case 1: No restriction
Any 4 people can be chosen from the 12 to be in th 1st group
Number of ways = $C(12, 4)$
Any 4 people can be chosen from the remaining 8 (12 − 4) to be in the 2nd group Number of ways = $C(8, 4)$
The remaining 4 people will be chosen from the remaining 4 (8 − 4) to be in the 3rd group Number of ways = $C(4, 4)$
$ \text{Number of ways} \\[3ex] = C(12, 4) * C(8, 4) * C(4, 4) \\[3ex] = \dfrac{12!}{(12 - 4)! * 4!} * \dfrac{8!}{(8 - 4)! * 4!} * \dfrac{4!}{(4 - 4)! * 4!} \\[5ex] = 495 * 70 * 1 \\[3ex] = 34650 \\[3ex] $ However:
The 3 groups are not labeled.
They are not distinguishable.
Because the groups are not distinguishable (not labeled/of the same size), there may be overcounting.
To account for overcounting (prevent duplicates) and ensure that each group is counted once, we have to find the number of ways of arranging the three groups, and use it to divide the initial result.
Number of ways to arrange these 3 groups = 3! = 6 ways
Number of ways of selecting 12 people into 3 groups of 4 people without any restriction
= 34650 ÷ 6
= 5775 ways
Case 2: Condition: Assume Anjie and Bubay are in the same group.
Type: Combination
1st: Anjie must be in the group: 1 spot is filled
Bubay must be in the group: another spot is filled
Two spots are filled.
We have to select 2 more people from 10 (12 − 2)
Number of ways = $1 * 1 * C(10, 2)$
= 45 ways
2nd: For the other two groups:
Any 4 people can be chosen from the remaining 8 (12 − 4) to be in the 2nd group Number of ways = $C(8, 4)$
The remaining 4 people will be chosen from the remaining 4 (8 − 4) to be in the 3rd group Number of ways = $C(4, 4)$
Because the two groups are not labeled (of the same size), the number of ways to arrange these 2 groups = 2! = 2 ways
Number of ways of dividing 8 people into 2 groups of 4 people
= $[C(8, 4) * C(4, 4)]$ ÷ 2
= (70 * 1) ÷ 2
= 35 ways
Therefore, the number of ways of selecting 12 people into 3 groups of 4 people where Anjie and Bubay must be in the same group
= 45 * 35
= 1575 ways
(b.) The number of ways of selecting 12 people into 3 groups of 4 people where Anjie and Bubay must not be in the same group
= Case 1 − Case 2
= 5775 − 1575
= 4200 ways
(a.) A group of 5 students is to be selected from the class.
Find the number of possible groups in the following cases.
(i.) There are no restrictions.
(ii.) The group includes both Abby and Ben.
(iii.) The group includes either Abby or Ben, but not both.
(b.) All 10 students are arranged in a line.
How many arrangements are possible if there are exactly three students between Abby and Ben?
(b.) All 10 students are arranged in a line.
There are exactly three students between Abby and Ben
Case 1: No restriction on how Abby and Ben seats
It can be Abby, ..., Ben or Ben, ..., Abby
Type: Permutation
$ \begin{array}{c c c c c} \stackrel{\Large Abby}{\rule{2cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large Ben}{\rule{1.5cm}{0.5mm}} \end{array} \\ \begin{array}{c c c c c} \stackrel{\Large Ben}{\rule{1.5cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large Abby}{\rule{2cm}{0.5mm}} \end{array} \\[3ex] $ Number of arrangements = 2! = 2 arrangements
Case 2: Any three students are selected to seat between Abby and Ben
Type: Combination
After Abby and Ben are seated, 3 students are chosen from 8 (10 − 2)
Number of ways to select 3 people from 8 people
= $C(8, 3)$
= 56 ways
Case 3: Seating the three students between Abby and Ben
Type: Permutation
Number of arrangements to seat the 3 students between Abby and Ben
= 3!
= 6 arrangements
Case 4: Seating the remaining students
Type: Permutation
We are done with seating 5 students (Abby, Ben, and 3 students)
These 5 students must sit together.
They are treated as a single unit.
The remaining 5 students (10 − 5) need to be seated
So, we are looking at seating 6 students ("5 as 1" + 5)
Number of arrangements
= 6!
= 720 arrangements
∴ The possible number of seating arrangements if there are exactly three students between Abby and Ben
= Case 1 * Case 2 * Case 3 * Case 4
= 2 * 56 * 6 * 720
= 483840 arrangements
Student: Is there a simpler way to do this question?
I'm not sure if I can remember all these steps
Teacher: We can use another approach.
The Gaps/Spaning approach ...
$ \underline{\text{2nd Approach: Gaps Method}} \\[3ex] Let: \\[3ex] Abby = A \\[3ex] Ben = B \\[3ex] \text{These are the possibilities for the seating: Abby before Ben} \\[3ex] \begin{array}{c c c c c} \stackrel{\Large A}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large B}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} \end{array} \\ \begin{array}{c c c c c} \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large A}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large B}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} \end{array} \\ \begin{array}{c c c c c} \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large A}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large B}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} \end{array} \\ \begin{array}{c c c c c} \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large A}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large B}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} \end{array} \\ \begin{array}{c c c c c} \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large A}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large B}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} \end{array} \\ \begin{array}{c c c c c} \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large A}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large B}{\rule{1cm}{0.5mm}} \end{array} $
$ \underline{\text{1st Possibility}} \\[3ex] \begin{array}{c c c c c} \stackrel{\Large 1}{\rule{1cm}{0.5mm}} & \stackrel{\Large 8}{\rule{1cm}{0.5mm}} & \stackrel{\Large 7}{\rule{1cm}{0.5mm}} & \stackrel{\Large 6}{\rule{1cm}{0.5mm}} & \stackrel{\Large 1}{\rule{1cm}{0.5mm}} & \stackrel{\Large 5}{\rule{1cm}{0.5mm}} & \stackrel{\Large 4}{\rule{1cm}{0.5mm}} & \stackrel{\Large 3}{\rule{1cm}{0.5mm}} & \stackrel{\Large 2}{\rule{1cm}{0.5mm}} & \stackrel{\Large 1}{\rule{1cm}{0.5mm}} \end{array} $
If we analyze the first possibility
Seat Number 1: A can be seated in 1 seat: 1 arrangement
Seat Number 5: B can be seated in 1 seat: 1 arrangement
Seat Number 2: Any of 8 students can seat in the first seat after A: 8 arrangements
Seat Number 3: Any of 7 students can seat in the second seat after A: 7 arrangements
Seat Number 4: Any of 6 students can seat in the third seat after A (directly before B): 6 arrangements
Seat Number 6: Any of 5 students can seat in the sixth seat: 5 arrangements
Seat Number 7: Any of 4 students can seat in the sixth seat: 4 arrangements
Seat Number 8: Any of 3 students can seat in the sixth seat: 3 arrangements
Seat Number 9: Any of 2 students can seat in the sixth seat: 2 arrangements
Seat Number 10: The 1 remaining student must seat in the tenth seat: 1 arrangement
$ \text{Number of arrangements for 1 possibility} \\[3ex] = 1 * 1 * 8! \\[3ex] = 8!\text{ arrangements} \\[3ex] $ Each possibility gives the same result.
There are 6 possibilities.
Ask students to list the arrangement of the remaining 5 possibilities.
$ \text{Number of arrangements for 6 possibilities} \\[3ex] = 6 * 8!\text{ arrangements} \\[5ex] \text{These are the possibilities for the seating: Ben before Abby} \\[3ex] \begin{array}{c c c c c} \stackrel{\Large B}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large A}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} \end{array} \\ \begin{array}{c c c c c} \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large B}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large A}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} \end{array} \\ \begin{array}{c c c c c} \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large B}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large A}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} \end{array} \\ \begin{array}{c c c c c} \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large B}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large A}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} \end{array} \\ \begin{array}{c c c c c} \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large B}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large A}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} \end{array} \\ \begin{array}{c c c c c} \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large B}{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large }{\rule{1cm}{0.5mm}} & \stackrel{\Large A}{\rule{1cm}{0.5mm}} \end{array} \\[5ex] \text{Number of arrangements for 6 possibilities} \\[3ex] = 6 * 8!\text{ arrangements} \\[5ex] \text{Total Number of possible arrangements} \\[3ex] = 2 * 6 * 8! \\[3ex] = 483840\text{ arrangements} $
Simplify each term as far as possible.
(b.) Find the term independent of x in the expansion of $\left(4x^2 + \dfrac{1}{2x^2}\right)^8$
$ (a.) \\[3ex] \underline{\text{1st 3 terms}} \\[3ex] \left(x + \dfrac{2}{x^2}\right)^{10} \\[5ex] = x^{10} + C(10, 1) * x^9 * \left(\dfrac{2}{x^2}\right) + C(10, 2) * x^8 * \left(\dfrac{2}{x^2}\right)^2 \\[5ex] = x^{10} + \dfrac{10!}{(10 - 1)! * 1!} * \dfrac{2x^9}{x^2} + \dfrac{10!}{(10 - 2)! * 2!} * x^8 * \dfrac{4}{x^4} \\[5ex] = x^{10} + 10 * 2 * x^{9 - 2} + 45 * 4 * x^{8 - 4} \\[4ex] = x^{10} + 20x^7 + 180x^4 \\[3ex] (b.) \\[3ex] \left(4x^2 + \dfrac{1}{2x^2}\right)^8 \\[5ex] $ The term independent of x is the term where the power of x in the numerator is equal to the power of x in the denominator, so they can divide to give 1
At the moment, they are the same power/degree/exponent, but will change when we begin to expand.
We do not need to expand the entire expression.
When we get to the expansion of the exponents by 4, we notice that the powers will cancel out: $x^8$ in the numerator is divided by $x^8$ in the denominator, leaving a result of 1.
This is the 5th term.
$ \text{5th term} \\[3ex] = C(8, 4) * (4x^2)^4 * \left(\dfrac{1}{2x^2}\right)^4 \\[5ex] = \dfrac{8!}{(8 - 4)! * 4!} * 256x^8 * \dfrac{1}{16x^8} \\[5ex] = \dfrac{70 * 256}{16} \\[5ex] = 1120 $
(b.) 6-digit numbers are to be formed using the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Each digit may be used only once in any 6-digit number.
A 6-digit number must not start with 0.
Find how many 6-digit numbers can be formed if:
(i.) there are no further restrictions.
(ii.) the 6-digit number is divisible by 10.
(iii.) the 6-digit number is greater than 500 000 and even.
(a.) Combination
The 4 groups containing 2, 3, 4 and 5 people is considered distinguishable (labeled) because of the different group sizes.
In that regard, overcounting is not taken into account.
Any 2 people can be chosen from the 14 to be in th 1st group
Number of ways = $C(14, 2)$
Any 3 people can be chosen from the remaining 12 (14 − 2) to be in the 2nd group Number of ways = $C(12, 3)$
Any 4 people can be chosen from the remaining 9 (12 − 3) to be in the 3rd group Number of ways = $C(9, 4)$
The remaining 5 people will be chosen from the remaining 5 (9 − 4) to be in the 4th group Number of ways = $C(5, 5)$
$ \text{Number of ways} \\[3ex] = C(14, 2) * C(12, 3) * C(9, 4) * C(5, 5) \\[3ex] = \dfrac{14!}{(14 - 2)! * 2!} * \dfrac{12!}{(12 - 3)! * 3!} * \dfrac{9!}{(9 - 4)! * 4!} * \dfrac{5!}{(5 - 5)! * 5!} \\[5ex] = 91 * 220 * 126 * 1 \\[3ex] = 2522520\;\;ways \\[3ex] $ (b.)(i.)
6-digit number
Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
There are 10 digits.
Restrictions:
(1.) No repetitions: each number may be used only once.
(2.) The 6-digit number must not start with 0.
This leaves us with 9 (10 − 1) digits.
(i.) No further restrictions.
Digit Number 1: Any of the 9 numbers besides 0 may be used as the 1st digit: 9 arrangements
0 must not be used, hence we have 9 numbers.
Digit Number 2: Any of remaining 8 numbers (8 arrangements from 9 − 1) and 0 (1 arrangement) can be used as the 2nd digit: 8 + 1 = 9 arrangements
Digit Number 3: Any of remaining 8 numbers may be used as the 3rd digit: 8 arrangements.
Digit Number 4: Any of remaining 7 numbers may be used as the 4th digit: 7 arrangements.
Digit Number 5: Any of remaining 6 numbers may be used as the 5th digit: 6 arrangements.
Digit Number 6: Any of remaining 5 numbers may be used as the 6th digit: 5 arrangements.
$ \begin{array}{c c c c c} \stackrel{\Large 9}{\rule{1cm}{0.5mm}} & \stackrel{\Large 9}{\rule{1cm}{0.5mm}} & \stackrel{\Large 8}{\rule{1cm}{0.5mm}} & \stackrel{\Large 7}{\rule{1cm}{0.5mm}} & \stackrel{\Large 6}{\rule{1cm}{0.5mm}} & \stackrel{\Large 5}{\rule{1cm}{0.5mm}} \end{array} \\[5ex] \text{Number of 6-digits that can be formed} \\[3ex] = 9 * 9 * 8 * 7 * 6 * 5 \\[3ex] = 136080 $
(ii.) The 6-digit number is divisible by 10.
Any number divisible by 10 must end with a 0
Digit Number 6: The 6th digit must be 0: 1 arrangement.
Digit Number 1: Any of the 9 numbers besides 0 may be used as the 1st digit: 9 arrangements
0 must not be used, and has already been used, hence we have 9 numbers.
Digit Number 2: Any of remaining 8 numbers may be used as the 2nd digit: 8 arrangements
Digit Number 3: Any of remaining 7 numbers may be used as the 3rd digit: 7 arrangements.
Digit Number 4: Any of remaining 6 numbers may be used as the 4th digit: 6 arrangements.
Digit Number 5: Any of remaining 5 numbers may be used as the 5th digit: 5 arrangements.
$ \begin{array}{c c c c c} \stackrel{\Large 9}{\rule{1cm}{0.5mm}} & \stackrel{\Large 8}{\rule{1cm}{0.5mm}} & \stackrel{\Large 7}{\rule{1cm}{0.5mm}} & \stackrel{\Large 6}{\rule{1cm}{0.5mm}} & \stackrel{\Large 5}{\rule{1cm}{0.5mm}} & \stackrel{\Large 1}{\rule{1cm}{0.5mm}} \end{array} \\[5ex] \text{Number of 6-digits that can be formed} \\[3ex] = 9 * 8 * 7 * 6 * 5 * 1 \\[3ex] = 15120 $
(iii.) The 6-digit number is greater than 500 000 and even.
In the context of the question:
A number greater than 500 000 must have the first digit as at least 5: from 5 through 9 (5, 6, 7, 8, 9): 5 arrangements
An even number is a number that must end in 0, 2, 4, 6, 8
There are overlap numbers for the two conditions: greater than 500 000 and even: 6, 8
Because of the overlap of these two numbers, we have to consider a case that involves only them (6, 8) as the 1st digit and a case that does not involve them (5, 7, 9) as the 1st digit.
Case 1: involves only 6, 8 as the 1st digit
Digit Number 1: Any of the 2 numbers (6, 8) may be used as the 1st digit: 2 arrangements
Digit Number 6: Any of the remaining 3 digits (5, 7, 9) and either 6 or 8 (depending on which one was used in the 1st digit) may be used as the 6th digit: 4 arrangements.
Digit Number 2: Any of remaining 8 numbers (10 − 1 − 1) may be used as the 2nd digit: 8 arrangements
Digit Number 3: Any of remaining 7 numbers may be used as the 3rd digit: 7 arrangements.
Digit Number 4: Any of remaining 6 numbers may be used as the 4th digit: 6 arrangements.
Digit Number 5: Any of remaining 5 numbers may be used as the 5th digit: 5 arrangements.
$\begin{array}{c c c c c} \stackrel{\Large 2}{\rule{1cm}{0.5mm}} & \stackrel{\Large 8}{\rule{1cm}{0.5mm}} & \stackrel{\Large 7}{\rule{1cm}{0.5mm}} & \stackrel{\Large 6}{\rule{1cm}{0.5mm}} & \stackrel{\Large 5}{\rule{1cm}{0.5mm}} & \stackrel{\Large 4}{\rule{1cm}{0.5mm}} \end{array} \\[5ex] \text{Number of 6-digits that can be formed in Case 1} \\[3ex] = 2 * 8 * 7 * 6 * 5 * 4 \\[3ex] = 13440 $
Case 2: does not involve 6, 8 as the 1st digit
Digit Number 1: Any of the 3 numbers (5, 7, 9) may be used as the 1st digit: 3 arrangements
Digit Number 6: Any of the 5 digits (0, 2, 4, 6, 8) may be used as the 6th digit: 5 arrangements.
Digit Number 2: Any of remaining 8 numbers (10 − 1 − 1) may be used as the 2nd digit: 8 arrangements
Digit Number 3: Any of remaining 7 numbers may be used as the 3rd digit: 7 arrangements.
Digit Number 4: Any of remaining 6 numbers may be used as the 4th digit: 6 arrangements.
Digit Number 5: Any of remaining 5 numbers may be used as the 5th digit: 5 arrangements.
$\begin{array}{c c c c c} \stackrel{\Large 3}{\rule{1cm}{0.5mm}} & \stackrel{\Large 8}{\rule{1cm}{0.5mm}} & \stackrel{\Large 7}{\rule{1cm}{0.5mm}} & \stackrel{\Large 6}{\rule{1cm}{0.5mm}} & \stackrel{\Large 5}{\rule{1cm}{0.5mm}} & \stackrel{\Large 5}{\rule{1cm}{0.5mm}} \end{array} \\[5ex] \text{Number of 6-digits that can be formed in Case 2} \\[3ex] = 3 * 8 * 7 * 6 * 5 * 5 \\[3ex] = 25200 \\[3ex] $ ∴ The number of 6-digits that can be formed if the 6-digit number is greater than 500 000 and even
= 13440 + 25200
= 38640
Find the values of n, p and q.
(b.) Find the term independent of y in the expansion of $\left(2y - \dfrac{1}{3y^2}\right)^6$.
Give your answer in exact form.
$ (a.) \\[3ex] (3 + px)^n = 243 + 810x + qx^2...\text{Given} \\[3ex] (3 + px)^n = 3^n + C(n, 1)(3^{n - 1})(px) + C(n, 2)(3^{n - 2})(px)^2 \\[3ex] \text{Compare}: \\[3ex] \underline{\text{1st term to 1st term}} \\[3ex] 3^n = 243 \\[3ex] 3^n = 3^5 \\[3ex] n = 5 \\[5ex] \underline{\text{2nd term to 2nd term}} \\[3ex] C(n, 1)(3^{n - 1})(px) = 810x \\[3ex] C(5, 1)(3^{5 - 1}) * p * x = 810x \\[3ex] \dfrac{5!}{(5 - 1)! * 1!} * 3^4 * p = 810 \\[5ex] 5 * 81 * p = 810 \\[3ex] p = \dfrac{810}{5 * 81} \\[5ex] p = 2 \\[5ex] \underline{\text{3rd term to 3rd term}} \\[3ex] C(n, 2)(3^{n - 2})(px)^2 = qx^2 \\[3ex] C(5, 2)(3^{5 - 2}) * p^2 * x^2 = qx^2 \\[3ex] \dfrac{5!}{(5 - 2)! * 2!} * 3^3 * 2^2 = q \\[5ex] 10 * 27 * 4 = q \\[3ex] q = 1080 \\[5ex] (b.) \\[3ex] \left(2y - \dfrac{1}{3y^2}\right)^6 \\[5ex] ........................................................... \\[3ex] \text{Let:} \\[3ex] \text{numerator} = n \\[3ex] \text{denominator} = d \\[3ex] \underline{\text{Expanded Term}} \\[3ex] \text{degree must be the same so they divide to be 1} \\[3ex] y^n \div y^{2d} = y^0 \\[3ex] y^{n - 2d} = y^0 \\[3ex] n - 2d = 0 \\[3ex] n = 2d ...eqn.(1) \\[5ex] \underline{\text{Each Term}} \\[3ex] n + d = 6 \\[3ex] 2d + d = 6 \\[3ex] 3d = 6 \\[3ex] d = \dfrac{6}{3} \\[5ex] d = 2 \implies \text{the 3rd term} \\[3ex] n = 2(2) = 4 \\[3ex] ........................................................... \\[3ex] \text{3rd term}\\[3ex] = C(6, 2) * (2y)^{6 - 2} * \left(-\dfrac{1}{3y^2}\right)^2 \\[5ex] = \dfrac{6!}{(6 - 2)! * 2!} * (2y)^4 * \dfrac{1}{9y^4} \\[5ex] = 15 * 16y^4 * \dfrac{1}{9y^4} \\[5ex] = \dfrac{80}{3} $
(i.) Find the number of different teams that can be chosen.
(ii.) Find the number of different teams that can be chosen if the group of 15 people contains a family of 4 people who must be kept together.
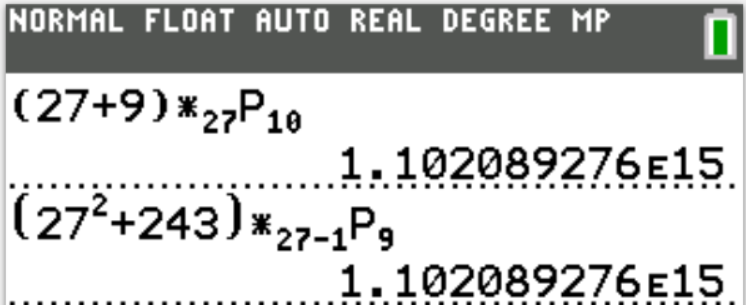
(b.) Given that $(n + 9) \times ^nP_{10} = (n^2 + 243) \times ^{(n - 1)}P_9$, find the value of n.
(a.)(i.)
Type: Combination
Number of different 8-people teams that can be chosen from a group of 15 people
$ = C(15, 8) \\[3ex] = \dfrac{15!}{(15 - 8)! * 8!} \\[5ex] = 6435\text{ teams} \\[3ex] $ (ii.)
Type: Combination
For the family of 4 people to be kept together, they may be in the 8-people team OR they may not be on the 8-people team.
The main thing is that the family of 4 must be together.
So, we shall consider: Case 1: where they are in the 8-people team; and Case 2: where they are not in the 8-people team.
Case 1: Family of 4 people must be kept together in the 8-people team chosen from a group of 15 people
Family of 4 being kept together: considered a single unit: 4 spots are filled
Number of ways to do it = C(4, 4) = 1 way
Remaining spots to be filled: 4 people (8 − 4) to be selected from 11 people (15 − 4)
Number of ways = C(11, 4)
$ \text{Number of ways for Case 1} \\[3ex] = 1 * C(11, 4) \\[3ex] = \dfrac{11!}{(11 - 4)! * 4!} \\[5ex] = 330\;ways \\[3ex] $ Case 2: Family of 4 people must be kept together but not in the 8-people team chosen from a group of 15 people
Family of 4 being kept together: considered a single unit: 4 spots are filled
Number of ways to do it = 1 way
Remaining spots to be filled: 8 people (8 − 4) to be selected from 11 people (15 − 4)
Number of ways = C(11, 8)
$ \text{Number of ways for Case 1} \\[3ex] = 1 * C(11, 8) \\[3ex] = \dfrac{11!}{(11 - 8)! * 8!} \\[5ex] = 165\;ways \\[5ex] \underline{\text{Number of ways for both cases}} \\[3ex] = 330 + 165 \\[3ex] = 495\;ways \\[3ex] $ The number of different teams that can be chosen if the group of 15 people contains a family of 4 people who must be kept together are 495 different 8-people teams.
$ (b.) \\[3ex] (n + 9) \times ^nP_{10} = (n^2 + 243) \times ^{(n - 1)}P_9 \\[3ex] (n + 9) \times P(n, 10) = (n^2 + 243) \times P(n - 1, 9) \\[3ex] ................................................................ \\[3ex] P(n, 10) = \dfrac{n!}{(n - 10)!} = \dfrac{n(n - 1)!}{(n - 10)!} \\[5ex] P(n - 1, 9) = \dfrac{(n - 1)!}{(n - 1 - 9)!} = \dfrac{(n - 1)!}{(n - 10)!} \\[5ex] ................................................................ \\[3ex] (n + 9) \times \dfrac{n(n - 1)!}{(n - 10)!} = (n^2 + 243) \times \dfrac{(n - 1)!}{(n - 10)!} \\[5ex] n(n + 9) = n^2 + 243 \\[3ex] n^2 + 9n - n^2 = 243 \\[3ex] n = \dfrac{243}{9} \\[5ex] n = 27 $
Simplify the coefficient of each term.
(ii.) The expansion of $7(1 + x)^n\left(1 + \dfrac{x}{7}\right)^5$, where n is a positive integer, is written in ascending powers of x.
The first two terms in the expansion are $7 + 89x$.
Find the value of n.
(b.) In the expansion of $(k - 2x)^8$, where k is a constant, the coefficient of $x^4$ divided by the coefficient of $x^2$ is $\dfrac{5}{8}$.
The coefficient of x is positive.
Form an equation and hence find the value of k.
$ (a.) (i.) \\[3ex] \left(1 + \dfrac{x}{7}\right)^5 \\[5ex] = 1^5 + C(5, 1) (1^4) \left(\dfrac{x}{7}\right) + C(5, 2) (1^3) \left(\dfrac{x}{7}\right)^2 \\[5ex] = 1 + \dfrac{5!}{(5 - 1)! * 1!} * 1 * \dfrac{x}{7} + \dfrac{5!}{(5 - 2)! * 2!} * \dfrac{x^2}{49} \\[5ex] = 1 + 5 * \dfrac{x}{7} + 10 * \dfrac{x^2}{49} \\[5ex] = 1 + \dfrac{5x}{7} + \dfrac{10x^2}{49} \\[5ex] (ii.) \\[3ex] 7(1 + x)^n\left(1 + \dfrac{x}{7}\right)^5 \\[5ex] \text{Let us do it two at a time; the first two terms} \\[3ex] \underline{\text{1st 2 expressions}} \\[3ex] 7(1 + x)^n \\[3ex] = 7[1^n + C(n, 1)(1^{n - 1})(x)] \\[3ex] = 7\left[1 + \dfrac{n!}{(n - 1)! * 1!} * x\right] \\[5ex] = 7\left[1 + \dfrac{n(n - 1)!}{(n - 1)! * 1} * x\right] \\[5ex] = 7(1 + nx) \\[3ex] = 7 + 7nx \\[5ex] \underline{\text{Multiply with the remaining expression; the first two terms}} \\[3ex] (7 + 7nx)\left(1 + \dfrac{5x}{7}\right) \\[5ex] = 7 + 5x + 7nx + 5nx^2 \\[3ex] = 7 + x(5 + 7n) + 5nx^2 ...\text{Computed} \\[3ex] = 7 + 89x ...\text{Given} \\[3ex] \text{Compare: Computed with Given} \\[3ex] 7 = 7 \\[3ex] 5 + 7n = 89 \\[3ex] 7n = 89 - 5 \\[3ex] 7n = 84 \\[3ex] n = \dfrac{84}{7} \\[5ex] n = 12 \\[5ex] (b.) \\[3ex] (-2x)^4 \text{ is found in the 5th term} \\[3ex] \text{5th term} \\[3ex] = C(8, 4) (k^4) (-2x)^4 \\[3ex] = \dfrac{8!}{(8 - 4)! * 4!} * k^4 * 16x^4 \\[5ex] = 70 * k^4 * 16 * x^4 \\[3ex] = 1120k^4x^4 \\[3ex] \text{coefficient of }x^4 = 1120k^4 \\[5ex] (-2x)^2 \text{ is found in the 3rd term} \\[3ex] \text{3rd term} \\[3ex] = C(8, 2) (k^6) (-2x)^2 \\[3ex] = \dfrac{8!}{(8 - 2)! * 2!} * k^6 * 4x^2 \\[5ex] = 28 * k^6 * 4 * x^2 \\[3ex] = 112k^6x^2 \\[3ex] \text{coefficient of }x^2 = 112k^6 \\[5ex] \text{coefficient of }x^4 \div \text{coefficient of }x^2 = \dfrac{5}{8} \\[5ex] \dfrac{1120k^4}{112k^6x^2} = \dfrac{5}{8} \\[5ex] \dfrac{10}{k^{6 - 4}} = \dfrac{5}{8} \\[5ex] \dfrac{10}{k^2} = \dfrac{5}{8} \\[5ex] 5k^2 = 10(8) \\[3ex] k^2 = \dfrac{10(8)}{5} \\[5ex] k^2 = 16 \\[3ex] k = \pm \sqrt{16} \\[3ex] k = \pm 4 \\[3ex] $ But: The coefficient of x is positive.
What is the coefficient of x?
$ (-2x)^1 \text{ is found in the 2nd term} \\[3ex] \text{2nd term} \\[3ex] = C(8, 1) (k^7) (-2x)^1 \\[3ex] = \dfrac{8!}{(8 - 1)! * 1!} * k^7 * (-2x) \\[5ex] = 8 * k^7 * -2 * x \\[3ex] \text{coefficient of }x = -16k^7 \\[5ex] k = \pm 4 \\[3ex] \text{When }k = 4 \\[3ex] \text{coefficient of }x = -16(4)^7...\text{ this is negative} \\[5ex] \text{When }k = -4 \\[3ex] \text{coefficient of }x = -16(-4)^7...\text{ this is positive} \\[3ex] \therefore k = -4 $
(a.) Find the number of teams that can be formed.
(b.) Find the number of teams that can be formed without teachers.
(c.) Find the number of teams that can be formed with the same number of doctors as teachers.
6 teachers, 5 doctors amd 4 police officers
= 6 + 5 + 4
= 15 people
(a.)
Type: Combination
Number of different 8-people teams that can be formed from 15 people
$ = C(15, 8) \\[3ex] = \dfrac{15!}{(15 - 8)! * 8!} \\[5ex] = 6435\text{ teams} \\[3ex] $ Without any teachers ⇒ 5 doctors amd 4 police officers
= 5 + 4
= 9 people
(b.)
Type: Combination
Number of different 8-people teams that can be formed from 9 people
$ = C(9, 8) \\[3ex] = \dfrac{9!}{(9 - 8)! * 8!} \\[5ex] = 9\text{ teams} \\[3ex] $ (c.)
The 8-people team is to be formed from a combination of teachers, doctors, and police officers.
The team must have the same number of doctors as teachers.
Let us consider the different possibilities that meet this requirement
*Case 1:*? 1 teacher, 1 doctor, and 6 (8 − 1 − 1) police officers
This will not work because there are only 4 police officers
Case 1: 2 teachers, 2 doctors, and 4 (8 − 2 − 2) police officers
Number of ways = C(6, 2) * C(5, 2) * C(4, 4)
OR
Case 2: 3 teachers, 3 doctors, and 2 (8 − 3 − 3) police officers
Number of ways = C(6, 3) * C(5, 3) * C(4, 2)
OR
Case 3: 4 teachers, 4 doctors, and 0 (8 − 4 − 4) police officers
Number of ways = C(6, 4) * C(5, 4)
Number of 8-people teams with the same number of doctors as teachers
$ = \text{Case 1} + \text{Case 2} + \text{Case 3} \\[3ex] = [C(6, 2) * C(5, 2) * C(4, 4)] + [C(6, 3) * C(5, 3) * C(4, 2)] + [C(6, 4) * C(5, 4)] \\[3ex] = \left[\dfrac{6!}{(6 - 2)! * 2!} * \dfrac{5!}{(5 - 2)! * 2!} * \dfrac{4!}{(4 - 4)! * 4!}\right] + \\[5ex] \left[\dfrac{6!}{(6 - 3)! * 3!} * \dfrac{5!}{(5 - 3)! * 3!} * \dfrac{4!}{(4 - 2)! * 2!}\right] + \\[5ex] \left[\dfrac{6!}{(6 - 4)! * 4!} * \dfrac{5!}{(5 - 4)! * 4!}\right] \\[5ex] = (15 * 10 * 1) + (20 * 10 * 6) + (15 * 5) \\[3ex] = 150 + 1200 + 75 \\[3ex] = 1425\text{ teams} $
Show that $a^2b = -12$ and find the value of a and the value of b.
The term independent of x implies that the exponent of x in the numerator should be equal to the exponent of x in the denominator. The x's (not your ex's lol) will cancel out.
Let:
numerator = n
denominator = d
$ \left(ax + \dfrac{b}{x^2}\right)^9 \\[5ex] ....................................................................... \\[3ex] \dfrac{x^n}{x^{2d}} \\[5ex] n = 2d ...eqn.(1)...\text{so the x's cancel out} \\[3ex] n + d = 9 ...eqn.(2) ...\text{based on the Binomial Theorem} \\[3ex] \implies \\[3ex] 2d + d = 9 \\[3ex] 3d = 9 \\[3ex] d = \dfrac{9}{3} \\[5ex] d = 3 \\[3ex] \text{From eqn.(2)} \\[3ex] n = 9 - d \\[3ex] n = 9 - 3 \\[3ex] n = 6 \\[3ex] \text{the term independent in }x \text{ is }: d = 3...\text{4th term} \\[3ex] ....................................................................... \\[3ex] \text{4th term} \\[3ex] = C(9, 3) * (ax)^6 * \left(\dfrac{b}{x^2}\right)^3 \\[5ex] = \dfrac{9!}{(9 - 3)! * 3!} * a^6 * x^6 * \dfrac{b^3}{x^6} \\[5ex] = 84a^6b^3 \\[3ex] 84a^6b^3 = -145152 \\[3ex] a^6b^3 = -\dfrac{145152}{84} \\[5ex] a^6b^3 = -1728 ...eqn.(3) \\[3ex] b^3 = -\dfrac{1728}{a^6} \\[5ex] b = \sqrt[3]{-\dfrac{1728}{a^6}} \\[5ex] b = \dfrac{\sqrt[3]{-1728}}{a^{6 * \dfrac{1}{3}}} \\[7ex] b = -\dfrac{12}{a^2}...eqn.(4) \\[5ex] a^2b = -12 \\[3ex] $ To get the coefficient of $x^6$, we need the term that has $x^6$
To get the term that has $x^6$, the numerator exponent minus the denominator exponent should be 6.
$ ....................................................................... \\[3ex] \dfrac{x^n}{x^{2d}} \\[5ex] n - 2d = 6 ...eqn.(5)...\text{to get the term with }x^6 \\[3ex] n + d = 9 ...eqn.(6) ...\text{based on the Binomial Theorem} \\[3ex] eqn.(6) - eqn.(5) \implies \\[3ex] 3d = 3 \\[3ex] d = \dfrac{3}{3} \\[5ex] d = 1 \\[3ex] \text{From eqn.(6)} \\[3ex] n = 9 - d \\[3ex] n = 9 - 1 \\[3ex] n = 8 \\[3ex] \text{the term with }x^6 \text{ is }: d = 1...\text{2nd term} \\[3ex] ....................................................................... \\[3ex] \text{2nd term} \\[3ex] = C(9, 1) * (ax)^8 * \left(\dfrac{b}{x^2}\right)^1 \\[5ex] = \dfrac{9!}{(9 - 1)! * 1!} * a^8 * x^8 * \dfrac{b^1}{x^2} \\[5ex] = 9a^8b * x^6 \\[3ex] \text{coefficient of }x^6 = 9a^8b \\[3ex] 9a^8b = -6912 \\[3ex] a^8b = -\dfrac{6912}{9} \\[5ex] a^8b = -768 ...eqn.(7) \\[5ex] \text{Substitute for b from eqn.(4)} \\[3ex] a^8 * -\dfrac{12}{a^2} = -768 \\[5ex] \dfrac{a^8}{a^2} = \dfrac{-768}{-12} \\[5ex] a^{8 - 2} = \dfrac{-768}{-12} \\[5ex] a^6 = 64 \\[3ex] a = \sqrt[6]{64} \\[3ex] a = 2 \\[3ex] \text{Substitute for a in eqn.(4)} \\[3ex] b = -\dfrac{12}{2^2} \\[5ex] b = -3 $
Each digit may be used only once in any 6-digit number.
A 6-digit number cannot start with 0.
(i.) Find how many 6-digit numbers can be formed.
(ii.) Find how many of these 6-digit numbers are divisible by 5.
(b.) A committee of 7 people is to be chosen from 6 doctors, 10 nurses and 8 dentists.
(i.) Find the number of committees that can be chosen.
(ii.) Find the number of committees that can be chosen if all the doctors have to be on the committee.
(iii.) Find the number of committees that can be chosen if there has to be at least one dentist on the committee.
6-digit number
Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
There are 10 digits.
Restrictions:
(1.) No repetitions: each digit may be used only once in any 6-digit number.
(2.) The 6-digit number must not start with 0.
This leaves us with 9 (10 − 1) digits.
(i.) Find how many 6-digit numbers can be formed.
Digit Number 1: Any of the 9 numbers besides 0 may be used as the 1st digit: 9 arrangements
0 must not be used, hence we have 9 numbers.
Digit Number 2: Any of remaining 8 numbers (8 arrangements from 9 − 1) and 0 (1 arrangement) can be used as the 2nd digit: 8 + 1 = 9 arrangements
Digit Number 3: Any of remaining 8 numbers may be used as the 3rd digit: 8 arrangements.
Digit Number 4: Any of remaining 7 numbers may be used as the 4th digit: 7 arrangements.
Digit Number 5: Any of remaining 6 numbers may be used as the 5th digit: 6 arrangements.
Digit Number 6: Any of remaining 5 numbers may be used as the 6th digit: 5 arrangements.
$ \begin{array}{c c c c c} \stackrel{\Large 9}{\rule{1cm}{0.5mm}} & \stackrel{\Large 9}{\rule{1cm}{0.5mm}} & \stackrel{\Large 8}{\rule{1cm}{0.5mm}} & \stackrel{\Large 7}{\rule{1cm}{0.5mm}} & \stackrel{\Large 6}{\rule{1cm}{0.5mm}} & \stackrel{\Large 5}{\rule{1cm}{0.5mm}} \end{array} \\[5ex] \text{Number of 6-digit numbers that can be formed} \\[3ex] = 9 * 9 * 8 * 7 * 6 * 5 \\[3ex] = 136080 $
(ii.) The 6-digit number is divisible by 5.
Any number divisible by 5 must end with a 0 or 5
Let us consider both cases: where the 6th digit ends with a 0 and where the 6th digit ends with a 5.
Case 1: where the 6th digit ends with a 0
Digit Number 6: The 6th digit must be 0: 1 arrangement
Digit Number 1: Any of the remaining 9 numbers may be used as the 1st digit: 9 arrangements
Digit Number 2: Any of remaining 8 numbers may be used as the 2nd digit: 8 arrangements
Digit Number 3: Any of remaining 7 numbers may be used as the 3rd digit: 7 arrangements.
Digit Number 4: Any of remaining 6 numbers may be used as the 4th digit: 6 arrangements.
Digit Number 5: Any of remaining 5 numbers may be used as the 5th digit: 5 arrangements.
$ \begin{array}{c c c c c} \stackrel{\Large 9}{\rule{1cm}{0.5mm}} & \stackrel{\Large 8}{\rule{1cm}{0.5mm}} & \stackrel{\Large 7}{\rule{1cm}{0.5mm}} & \stackrel{\Large 6}{\rule{1cm}{0.5mm}} & \stackrel{\Large 5}{\rule{1cm}{0.5mm}} & \stackrel{\Large 1}{\rule{1cm}{0.5mm}} \end{array} \\[5ex] \text{Number of 6-digits that can be formed from Case 1} \\[3ex] = 9 * 8 * 7 * 6 * 5 * 1 \\[3ex] = 15120 \\[3ex] $ OR
Case 2: where the 6th digit ends with a 5
Digit Number 6: The 6th digit must be 5: 1 arrangement
Digit Number 1: Any of the remaining 9 numbers besides 0 may be used as the 1st digit: 8 arrangements
0 must not be used as the 1st digit; 5 has already been used as the last digit, hence we have 8 arrangements.
Digit Number 2: Any of remaining 8 numbers may be used as the 2nd digit: 8 arrangements
Digit Number 3: Any of remaining 7 numbers may be used as the 3rd digit: 7 arrangements.
Digit Number 4: Any of remaining 6 numbers may be used as the 4th digit: 6 arrangements.
Digit Number 5: Any of remaining 5 numbers may be used as the 5th digit: 5 arrangements.
$ \begin{array}{c c c c c} \stackrel{\Large 8}{\rule{1cm}{0.5mm}} & \stackrel{\Large 8}{\rule{1cm}{0.5mm}} & \stackrel{\Large 7}{\rule{1cm}{0.5mm}} & \stackrel{\Large 6}{\rule{1cm}{0.5mm}} & \stackrel{\Large 5}{\rule{1cm}{0.5mm}} & \stackrel{\Large 1}{\rule{1cm}{0.5mm}} \end{array} \\[5ex] \text{Number of 6-digits that can be formed from Case 2} \\[3ex] = 8 * 8 * 7 * 6 * 5 * 1 \\[3ex] = 13440 \\[3ex] $ Number of 6-digit numbers are divisible by 5
= Case 1 + Case 2
= 15120 + 13440
= 28560
(b.) 6 doctors, 10 nurses, and 8 dentists
= 6 + 10 + 8
= 24 people
(i.)
Type: Combination
Number of 7-person committee that can be chosen from 24 people
$ = C(24, 7) \\[3ex] = \dfrac{24!}{(24 - 7)! * 7!} \\[5ex] = 346104\text{ committees} \\[3ex] $ (ii.) All the doctors have to be on the committee.
6 doctors; 7-person committee
Case 1: Choose 6 doctors from 6 doctors
Number of ways = C(6, 6)
AND
Case 2: Choose the remaining committee person (7 − 6) from the remaining people: 18 (10 nurses + 8 dentists)
Number of ways = C(18, 1)
$ \text{Number of committees if all the doctors have to be on the committee.} \\[3ex] = \text{Case 1} * \text{Case 2} \\[3ex] = C(6, 6) * C(18, 1) \\[3ex] = \dfrac{6!}{(6 - 6)! * 6!} * \dfrac{18!}{(18 - 1)! * 1!} \\[5ex] = 1 * 18 \\[3ex] = 346104\text{ committees} \\[3ex] $ (iii.) Number of committees if there has to be at least one dentist on the committee.
We can solve this question using at least two approches.
Use any approach you prefer.
1st Approach: Complementary Rule
Let:
Case 3 = Number of committees if there has to be at least one dentist on the committee
Case 4 = Number of committees if there is no dentist on the committee
Case 5 = Number of committees that can be chosen.
Number of committees if there has to be at least one dentist on the committee
+
Number of committees if there is no dentist on the committee
=
Number of committees that can be chosen.
Case 4:
6 doctors and 10 nurses
= 6 + 10
= 16 people
Number of 7-person committee that can be chosen from 16 people
$ = C(16, 7) \\[3ex] = \dfrac{16!}{(16 - 7)! * 7!} \\[5ex] = 11440\text{ committees} \\[3ex] $ Case 5:
Number of 7-person committee that can be chosen from 24 people = 346104 committees
∴ Case 3:
Number of committees if there is no dentist on the committee
= Case 5 − Case 4
= 346104 − 11440
= 334664
2nd Approach: By Definition
This approach involves more work, but some people may find it easier to understand.
At least one means one or more
In the context of the question: For a 7-person committee, at least 1 dentist means 1, 2, 3, 4, 5, 6, 7
$ \text{6 doctors, 10 nurses and 8 dentists: 7-person committee} \\[3ex] \text{8 dentists; 16 (10 + 6) nurses and doctors} \\[5ex] \text{1 dentist AND 6 nurses and doctors} \\[3ex] = C(8, 1) * C(16, 6) \\[3ex] = 8 * 8008 \\[3ex] = 64064 \\[3ex] OR \\[3ex] \text{2 dentists AND 5 nurses and doctors} \\[3ex] = C(8, 2) * C(16, 5) \\[3ex] = 28 * 4368 \\[3ex] = 122304 \\[3ex] OR \\[3ex] \text{3 dentists AND 4 nurses and doctors} \\[3ex] = C(8, 3) * C(16, 4) \\[3ex] = 56 * 1820 \\[3ex] = 101920 \\[3ex] OR \\[3ex] \text{4 dentists AND 3 nurses and doctors} \\[3ex] = C(8, 4) * C(16, 3) \\[3ex] = 70 * 560 \\[3ex] = 39200 \\[3ex] OR \\[3ex] \text{5 dentists AND 2 nurses and doctors} \\[3ex] = C(8, 5) * C(16, 2) \\[3ex] = 56 * 120 \\[3ex] = 6720 \\[3ex] OR \\[3ex] \text{6 dentists AND 1 nurse/doctor} \\[3ex] = C(8, 6) * C(16, 1) \\[3ex] = 28 * 16 \\[3ex] = 448 \\[3ex] OR \\[3ex] \text{7 dentists AND 0 nurse/doctor} \\[3ex] = C(8, 7) * C(16, 0) \\[3ex] = 8 * 1 \\[3ex] = 8 \\[3ex] \implies \\[3ex] \text{Number of committees if at least one dentist is on the committee} \\[3ex] = 64064 + 122304 + 101920 + 39200 + 6720 + 448 + 8 \\[3ex] = 334664 $
Find the values of n, p and q.
(b.) Find the term independent of x in the expansion of $\left(\dfrac{2}{x^2} + \dfrac{x}{3}\right)^6$, giving your answer as a rational number.
$ (a.) \\[3ex] \left(1 - \dfrac{x}{2}\right)^n \\[5ex] = 1^n + C(n, 1)(1)^{n - 1}\left(-\dfrac{x}{2}\right)^1 + C(n, 2)(1)^{n - 2}\left(-\dfrac{x}{2}\right)^2 + C(n, 3)(1)^{n - 3}\left(-\dfrac{x}{2}\right)^3 \\[5ex] .................................................................................. \\[3ex] C(n, 1) \\[3ex] = \dfrac{n!}{(n - 1)! * 1!} \\[5ex] = \dfrac{n(n - 1)!}{(n - 1)!} \\[5ex] = n \\[5ex] C(n, 2) \\[3ex] = \dfrac{n!}{(n - 2)! * 2!} \\[5ex] = \dfrac{n(n - 1)(n - 2)!}{2(n - 2)!} \\[5ex] = \dfrac{n(n - 1)}{2} \\[5ex] C(n, 3) \\[3ex] = \dfrac{n!}{(n - 3)! * 3!} \\[5ex] = \dfrac{n(n - 1)(n - 2)(n - 3)!}{6(n - 3)!} \\[5ex] = \dfrac{n(n - 1)(n - 2)}{6} \\[5ex] .................................................................................. \\[3ex] = 1 + n(1)\left(-\dfrac{x}{2}\right) + \dfrac{n(n - 1)}{2}(1)\left(\dfrac{x^2}{4}\right) + \dfrac{n(n - 1)(n - 2)}{6}(1)\left(-\dfrac{x^3}{8}\right) \\[5ex] = 1 - \dfrac{n}{2}x + \dfrac{n(n - 1)}{8}x^2 - \dfrac{n(n - 1)(n - 2)}{48}x^3...\text{Calculated} \\[5ex] = 1 - 8x + px^2 + qx^3 ...\text{Given} \\[3ex] \text{Calculated = Given: Compare} \\[3ex] \dfrac{n}{2} = 8 \\[5ex] n = 2(8) \\[3ex] n = 16 \\[5ex] \dfrac{n(n - 1)}{8} = p \\[5ex] p = \dfrac{16(16 - 1)}{8} \\[5ex] p = 2(15) \\[3ex] p = 30 \\[5ex] -\dfrac{n(n - 1)(n - 2)}{48} = q \\[5ex] q = -\dfrac{16(16 - 1)(16 - 2)}{48} \\[5ex] q = -5(14) \\[3ex] q = -70 \\[3ex] $ The term independent of x implies that the exponent of x in the numerator (2nd term) should be equal to the exponent of x in the denominator (1st term).
The x's will cancel out.
Let:
numerator = n
denominator = d
$ \left(\dfrac{2}{x^2} + \dfrac{x}{3}\right)^6 \\[5ex] ....................................................................... \\[3ex] \dfrac{x^n}{x^{2d}} \\[5ex] n = 2d ...eqn.(1)...\text{so the x's cancel out} \\[3ex] n + d = 6 ...eqn.(2) ...\text{based on the Binomial Theorem} \\[3ex] \text{Substitute for n from eqn.(1) into eqn.(2)} \\[3ex] 2d + d = 6 \\[3ex] 3d = 6 \\[3ex] d = \dfrac{6}{3} \\[5ex] d = 2 \\[3ex] \text{From eqn.(1)} \\[3ex] n = 2(2) \\[3ex] n = 4 \\[3ex] \text{the term independent in }x \text{ is }: n = 4...\text{5th term} \\[3ex] ....................................................................... \\[3ex] (b.) \\[3ex] \text{5th term} \\[3ex] = C(6, 4) * \left(\dfrac{2}{x^2}\right)^2 * \left(\dfrac{x}{3}\right)^4 \\[5ex] = \dfrac{6!}{(6 - 4)! * 4!} * \dfrac{4}{x^4} * \dfrac{x^4}{81} \\[5ex] = \dfrac{20}{27} $
Letters: A B C X Y Z
Symbols: * $ # &
No character can be used more than once in any 5-character password.
(i.) Find the number of passwords that can be formed.
(ii.) Find the number of passwords that can be formed if the password has to contain at least one symbol.
(iii.) Find the number of passwords that can be formed if the password has to start with two letters and end with two symbols.
(b.) A team of 8 people is to be chosen from 5 doctors, 4 teachers and 6 police officers.
Find how many possible teams have the same number of doctors as teachers.
(a.)
6 letters
4 symbols
Sum = 10 characters (letters and symbols).
Restriction:
No character may be used more than once in any 5-character password.
(i.) Find the number of passwords that can be formed.
Type: Permutation (because the order matters: ABC*# is the not the same as B*A#C)
Number of 5-character passwords that can be formed
= P(10, 5)
= 30240 passwords
This is the explanation.
Character Number 1: Any of the 10 characters may be used as the 1st character: 10 arrangements.
Character Number 2: Any of the remaining 9 characters may be used as the 2nd character: 9 arrangements.
Character Number 3: Any of remaining 8 characters may be used as the 3rd character: 8 arrangements.
Character Number 4: Any of remaining 7 characters may be used as the 4th character: 7 arrangements.
Character Number 5: Any of remaining 6 characters may be used as the 5th character: 6 arrangements.
$ \begin{array}{c c c c c} \stackrel{\Large 10}{\rule{1cm}{0.5mm}} & \stackrel{\Large 9}{\rule{1cm}{0.5mm}} & \stackrel{\Large 8}{\rule{1cm}{0.5mm}} & \stackrel{\Large 7}{\rule{1cm}{0.5mm}} & \stackrel{\Large 6}{\rule{1cm}{0.5mm}} \end{array} \\[5ex] \text{Number of 5-character passwords that can be formed} \\[3ex] = 10 * 9 * 8 * 7 * 6 \\[3ex] = 30240\text{ passwords} \\[3ex] $ (ii.) Find the number of passwords that can be formed if the password has to contain at least one symbol.
We can solve this question using at least two approches.
Use any approach you prefer.
Complementary Rule
Type: Permutation (because the order matters)
Let:
Case 1 = Number of 5-character passwords that can be formed.
Case 2 = Number of 5-character passwords that can be formed without any symbol
Case 3 = Number of 5-character passwords that can be formed with at least one symbol.
Number of 5-character passwords that can be formed with at least one symbol (Case 2)
+
Number of 5-character passwords that can be formed without any symbol (Case 3)
=
Number of 5-character passwords that can be formed (Case 1)
Case 2 + Case 3 = Case 1
Case 3 = Case 1 − Case 2
6 letters
4 symbols
Sum = 10 characters (letters and symbols).
Case 1:
Number of 5-character passwords that can be formed
= P(10, 5)
= 30240 passwords
Case 2:
Number of 5-character passwords that can be formed without any symbol
= Number of 5-character passwords that can be formed with all letters
= P(6, 5)
= 720 passwords
Case 3:
Number of 5-character passwords that can be formed with at least one symbol
= 30240 − 720
= 29520 passwords
(iii.) The number of passwords that can be formed if the password has to start with two letters and end with two symbols.
Type: Permutation
Character Number 1: Any of the 6 letters may be used as the 1st character: 6 arrangements.
Character Number 2: Any of the remaining 5 letters may be used as the 2nd character: 5 arrangements.
Character Number 4: Any of the 4 symbols may be used as the 4th character: 4 arrangements.
Character Number 5: Any of remaining 3 symbols may be used as the 5th character: 3 arrangements.
Character Number 3: Any of remaining 6 (10 − 2 − 2) characters may be used as the 3rd character: 6 arrangements.
$ \begin{array}{c c c c c} \stackrel{\Large 6}{\rule{1cm}{0.5mm}} & \stackrel{\Large 5}{\rule{1cm}{0.5mm}} & \stackrel{\Large 6}{\rule{1cm}{0.5mm}} & \stackrel{\Large 4}{\rule{1cm}{0.5mm}} & \stackrel{\Large 3}{\rule{1cm}{0.5mm}} \end{array} \\[5ex] \text{Number of 5-character passwords that can be formed} \\[3ex] = 6 * 5 * 6 * 4 * 3 \\[3ex] = 2160\text{ passwords} \\[3ex] $ (b.)
The 8-people team is to be formed from a combination of 5 doctors, 4 teachers and 6 police officers.
The team must have the same number of doctors as teachers.
Let us consider the different possibilities that meet this requirement.
Case 1: 1 doctor, 1 teacher, and 6 (8 − 1 − 1) police officers
Number of ways = C(5, 1) * C(4, 1) * C(6, 6)
= 5 * 4 * 1
= 20 teams
OR
Case 2: 2 doctors, 2 teachers, and 4 (8 − 2 − 2) police officers
Number of ways = C(5, 2) * C(4, 2) * C(6, 4)
= 10 * 6 * 15
= 900 teams
OR
Case 3: 3 doctors, 3 teachers, and 2 (8 − 3 − 3) police officers
Number of ways = C(5, 3) * C(4, 3) * C(6, 2)
= 10 * 4 * 15
= 600 teams
OR
Case 4: 4 doctors, 4 teachers, and 0 (8 − 4 − 4) police officers
Number of ways = C(5, 4) * C(4, 4)
= 5 * 1
= 5 teams
Number of 8-people teams with the same number of doctors as teachers
= 20 + 900 + 600 + 5
= 1525 teams


