Junior Level Science Scholarship (JLSS) Resources
Welcome to Our Site
I greet you this day,
These are the solutions to the Junior Level Science Scholarship (JLSS) Examination sample tests.
If you find these resources valuable and if any of these resources were helpful in your passing the
JLSS exam, please consider making a donation:
Cash App: $ExamsSuccess or
cash.app/ExamsSuccess
PayPal: @ExamsSuccess or
PayPal.me/ExamsSuccess
Google charges me for the hosting of this website and my other
educational websites. It does not host any of the websites for free.
Besides, I spend a lot of time to type the questions and the solutions well.
As you probably know, I provide clear explanations on the solutions.
Your donation is appreciated.
Comments, ideas, areas of improvement, questions, and constructive
criticisms are welcome.
Feel free to contact me. Please be positive in your message.
I wish you the best.
Thank you.
$ a.\;\; 16 \\[3ex] b.\;\; 4 \\[3ex] c.\;\; 8 \\[3ex] d.\;\; 2\sqrt{2} \\[3ex] $
$ x^2 + y^2 + 4x - 6y - 3 = 0 \\[3ex] x^2 + 4x + y^2 - 6y = 3 \\[3ex] ....................................... \\[3ex] \text{coefficient of }x = 4 \\[3ex] \text{half of it} = \dfrac{1}{2} * 4 = 2 \\[5ex] \text{square it} = 2^2 \\[5ex] \text{coefficient of }y = -6 \\[3ex] \text{half of it} = \dfrac{1}{2} * -6 = -3 \\[5ex] \text{square it} = (-3)^2 \\[3ex] ....................................... \\[3ex] x^2 + 4x + 2^2 + y^2 - 6y + (-3)^2 = 3 + 2^2 + (-3)^2 \\[3ex] (x + 2)^2 + (y - 3)^2 = 3 + 4 + 9 \\[3ex] (x + 2)^2 + (y - 3)^2 = 16 \\[3ex] (x + 2)^2 + (y - 3)^2 = 4^2 \\[3ex] \text{Compare to the standard form: } (x - a)^2 + (y - b)^2 = r^2 \\[3ex] r = \text{radius} = 4 $
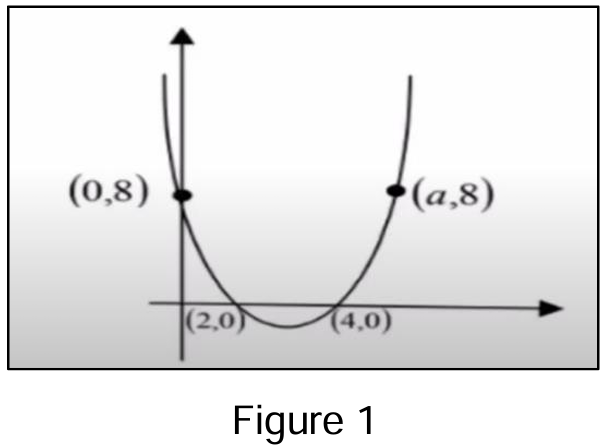
In Figure 1, the x-intercepts of a parabola are 2 and 4, and the y-intercept is 8.
If the parabola passes through the point (a, 8), what is the value of a?
$ a.\;\; 8 \\[3ex] b.\;\; 7 \\[3ex] c.\;\; 6 \\[3ex] d.\;\; 5 \\[3ex] $
$ x-\text{intercepts} = (2, 0) \hspace{2em}\text{and}\hspace{2em} (4, 0) \\[3ex] \text{zeros} = 2, 4 \\[3ex] \text{factors} = (x - 2)(x - 4) \\[3ex] \implies \\[3ex] y = k(x - 2)(x - 4)...\text{k is the leading coefficient} \\[3ex] y-\text{intercept} = (0, 8) \\[3ex] \text{passes through } (0, 8) \\[3ex] \text{To find leading coefficient, k} \\[3ex] x = 0,\hspace{3em} y = 8 \\[3ex] \implies \\[3ex] 8 = k(0 - 2)(0 - 4) \\[3ex] 8 = 8k \\[3ex] 8k = 8 \\[3ex] k = \dfrac{8}{8} \\[5ex] k = 1 \\[3ex] \implies \\[3ex] y = 1(x - 2)(x - 4) \\[3ex] y = (x - 2)(x - 4) \\[3ex] \text{Also}: \\[3ex] \text{passes through } (a, 8) \\[3ex] x = a,\hspace{3em} y = 8 \\[3ex] \implies \\[3ex] 8 = (a - 2)(a - 4) \\[3ex] a^2 - 4a - 2a + 8 = 8 \\[3ex] a^2 - 6a = 8 - 8 \\[3ex] a(a - 6) = 0 \\[3ex] a = 0 \hspace{2em}\text{OR}\hspace{2em} a - 6 = 0 \\[3ex] a = 0 \hspace{2em}\text{OR}\hspace{2em} a = 6 \\[3ex] \text{Point 1} = y-\text{intercept} = (0, 8) \\[3ex] \text{Point 2} = (a, 8) = (6, 8) \\[3ex] a = 6 $
$ a.\;\; 17 \\[3ex] b.\;\; 15 \\[3ex] c.\;\; 16 \\[3ex] d.\;\; 18 \\[3ex] $
The sum of the first n natural numbers is: $\text{Sum} = \dfrac{n(n + 1)}{2} \\[5ex]$ Therefore, the sum of the first x natural numbers is:
$ \text{Sum} = \dfrac{x(x + 1)}{2} \\[5ex] \dfrac{x(x + 1)}{2} = 171 \\[5ex] x(x + 1) = 2(171) \\[3ex] x^2 + x - 342 = 0 \\[3ex] (x + 19)(x - 18) = 0 \\[3ex] x + 19 = 0 \hspace{2em}\text{OR}\hspace{2em} x - 18 = 0 \\[3ex] x = -19 \hspace{2em}\text{OR}\hspace{2em} x = 18 \\[3ex] \text{Because the sum is a positive number; } x = 18 \\[3ex] $ Student: Mr. C
Teacher: Yes dear Student
Student: What if I did not memorize the sum of the first n natural numbers?
Or what if I do not know the formula?
Teacher: The sequence is an Arithmetic Sequence.
So, we can derive the formula for the sequence based on the formula for the Sum of Arithmetic Sequence.
Let's do it.
$ 1 + 2 + 3 + 4 + 5 + ... + x \\[3ex] \text{first term, } a = 1 \\[3ex] \text{common difference, } d = 2 - 1 = 1 \\[3ex] \text{number of terms, } n = x \\[3ex] \text{sum of n terms of an Arithmetic Sequence, } SAS_n = SAS_x \\[3ex] \implies \\[3ex] SAS_x = \dfrac{x}{2}[2a + d(x - 1)] \\[5ex] = \dfrac{x}{2}[2(1) + 1(x - 1)] \\[5ex] = \dfrac{x}{2}(2 + x - 1) \\[5ex] = \dfrac{x}{2}(x + 1) \\[5ex] = \dfrac{x(x + 1)}{2} $
Let α, β be the roots of the equation (replacing a and b respectively in the question).
$ (x - 2)(x - 3) + (x - 3)(x + 1) + (x + 1)(x - 2) = 0 \\[3ex] (x - 3)[(x - 2) + (x + 1)] + (x + 1)(x - 2) = 0 \\[3ex] (x - 3)(x - 2 + x + 1) + (x + 1)(x - 2) = 0 \\[3ex] (x - 3)(2x - 1) + (x + 1)(x - 2) = 0 \\[3ex] 2x^2 - x - 6x + 3 + x^2 - 2x + x - 2 = 0 \\[3ex] 3x^2 - 8x + 1 = 0 \\[3ex] \text{Compare to the standard form: } ax^2 + bx + c = 0 \\[3ex] a = 3 \\[3ex] b = -8 \\[3ex] c = 1 \\[3ex] \text{Sum of roots, } \alpha + \beta = -\dfrac{b}{a} = -\dfrac{-8}{3} = \dfrac{8}{3} \\[5ex] \text{Product of roots, } \alpha\beta = \dfrac{c}{a} = \dfrac{1}{3} \\[5ex] (\alpha + 1)(\beta + 1) \\[3ex] = \alpha\beta + \alpha + \beta + 1 \\[5ex] = \dfrac{1}{3} + \dfrac{8}{3} + \dfrac{3}{3} \\[5ex] = \dfrac{1 + 8 + 3}{3} \\[5ex] = \dfrac{12}{3} \\[5ex] = 4 \\[5ex] (\alpha - 2)(\beta - 2) \\[3ex] = \alpha\beta -2\alpha - 2\beta + 4 \\[5ex] = \alpha\beta -2(\alpha + \beta) + 4 \\[5ex] = \dfrac{1}{3} - 2\left(\dfrac{8}{3}\right) + \dfrac{12}{3} \\[5ex] = \dfrac{1 - 16 + 12}{3} \\[5ex] = -\dfrac{3}{3} \\[5ex] = -1 \\[5ex] (\alpha - 3)(\beta - 3) \\[3ex] = \alpha\beta -3\alpha - 3\beta + 9 \\[5ex] = \alpha\beta -3(\alpha + \beta) + 9 \\[5ex] = \dfrac{1}{3} - 3\left(\dfrac{8}{3}\right) + \dfrac{27}{3} \\[5ex] = \dfrac{1 - 24 + 27}{3} \\[5ex] = \dfrac{4}{3} \\[5ex] \implies \\[3ex] \dfrac{1}{(\alpha + 1)(\beta + 1)} + \dfrac{1}{(\alpha - 2)(\beta - 2)} + \dfrac{1}{(\alpha - 3)(\beta - 3)} \\[5ex] = \dfrac{1}{4} + \dfrac{-1}{1} + \dfrac{3}{4} \\[5ex] = \dfrac{1}{4} - \dfrac{4}{4} + \dfrac{3}{4} \\[5ex] = \dfrac{0}{4} \\[5ex] = 0 $
$ I.\;\; x^2 + y^2 = 4 \\[3ex] II.\;\; x - y = 4x \\[3ex] III.\;\; y = \sqrt{4} - x \\[3ex] IV.\;\; x = y^2 - y - 6 \\[3ex] V.\;\; y = x^2 + 5x + 6 \\[3ex] VI.\;\; x^2 = y^2 \\[5ex] a.\;\; II, III, IV \\[3ex] b.\;\; II, III, V \\[3ex] c.\;\; I, IV, VI \\[3ex] d.\;\; I, II, III \\[3ex] $
$ I.\;\; x^2 + y^2 = 4 \\[3ex] x^2 = 4 - y^2 \\[3ex] x = \pm\sqrt{4 - y^2}...\text{This is NOT a function} \\[5ex] II.\;\; x - y = 4x \\[3ex] y = x - 4x \\[3ex] y = -3x ...\text{This is a linear function} \\[5ex] III.\;\; y = \sqrt{4} - x...\text{This is a linear function} \\[5ex] IV.\;\; x = y^2 - y - 6 \\[3ex] y^2 = x + y + 6 \\[3ex] y = \pm \sqrt{x + y + 6} ...\text{This is NOT a function} \\[5ex] V.\;\; y = x^2 + 5x + 6 ...\text{This is a quadratic function} \\[5ex] VI.\;\; x^2 = y^2 \\[3ex] y = \pm\sqrt{x^2} ...\text{This is NOT a function} \\[5ex] The functions are: b.\;\; II, III, V $
You pick one marble from the jar.
Find the theoretical probability, P(blue or green)
$ a.\;\; \dfrac{4}{5} \\[5ex] b.\;\; \dfrac{1}{21} \\[5ex] c.\;\; \dfrac{2}{5} \\[5ex] d.\;\; \dfrac{3}{20} \\[5ex] $
Let the:
Sample Space = S
blue = B
red = R
green = G
$ n(B) = 12 \\[3ex] n(R) = 8 \\[3ex] n(G) = 20 \\[3ex] S = \{12B, 8R, 20G\} \\[3ex] n(S) = 12 + 8 + 20 = 40 \\[3ex] P(B or G) = P(B) + P(G) ...\text{Addition Rule for Independent Events} \\[3ex] = \dfrac{n(B)}{n(S)} + \dfrac{n(G)}{n(S)} \\[5ex] = \dfrac{12}{40} + \dfrac{20}{40} \\[5ex] = \dfrac{32}{40} \\[5ex] = \dfrac{4}{5} $
$ a.\;\; \sqrt{11} \pm 3 \\[3ex] b.\;\; \pm 3 \\[3ex] c.\;\; 3 \pm \sqrt{11} \\[3ex] d.\;\; -3 \pm \sqrt{11} \\[3ex] $
$ x^2 + 6x - 2 = 0 \\[3ex] x^2 + 6x = 2 \\[3ex] \text{coefficient of }x = 6 \\[3ex] \text{half of it} = \dfrac{1}{2} * 6 = 3 \\[5ex] \text{square it} = 3^2 \\[3ex] \implies \\[3ex] x^2 + 6x + 3^2 = 2 + 3^2 \\[3ex] (x + 3)^2 = 2 + 9 \\[3ex] x + 3 = \pm\sqrt{11} \\[3ex] x = -3 \pm\sqrt{11} $
What is the probability that you will answer all five questions correctly?
$ a.\;\; \dfrac{1}{40} \\[5ex] b.\;\; \dfrac{1}{6} \\[5ex] c.\;\; \dfrac{1}{1024} \\[5ex] d.\;\; \dfrac{1}{20} \\[5ex] $
Let:
S = sample space
E = event space
$ n(S) = 4 ...\text{4 choices} \\[3ex] n(E) = 1 ...\text{1 correct option} \\[3ex] P(E) = \dfrac{n(E)}{n(S)} = \dfrac{1}{4} ...\text{probability of answering one question correctly} \\[5ex] \text{The probability of answering five questions correctly} \\[3ex] = \left(\dfrac{1}{4}\right)^5...\text{Multiplication Rule for Independent Events} \\[5ex] = \dfrac{1}{1024} $
$ a.\;\; y = (x + 9)^2 + 2 \\[3ex] b.\;\; y = (x - 12)^2 - 16 \\[3ex] c.\;\; y = 2(x - 9)^2 - 2 \\[3ex] d.\;\; y = 3(x + 12)^2 + 16 \\[3ex] $
$ y = a(x - h)^2 + k ...\text{Vertex Form of a Quadratoc Function} \\[3ex] Vertex = (h, k) = (9, -2) \\[3ex] h = 9 \\[3ex] k = -2 \\[3ex] Point = (x, y) = (12, 16) \\[3ex] x = 12 \\[3ex] y = 16 \\[3ex] \text{Find the leading coefficient, }a \\[3ex] 16 = a(12 - 9)^2 + -2 \\[3ex] 16 = 9a - 2 \\[3ex] 9a = 16 + 2 \\[3ex] 9a = 18 \\[3ex] a = \dfrac{18}{9} \\[5ex] a = 2 \\[3ex] \implies \\[3ex] y = 2(x - 9)^2 + -2 \\[3ex] y = 2(x - 9)^2 - 2 $
What is the point on the circle opposite the point (0, 2), which is also on the circle?
$ a.\;\; (2, 0) \\[3ex] b.\;\; (4, 2) \\[3ex] c.\;\; (0, -2) \\[3ex] d.\;\; \\[3ex] $
$ (x - 2)^2 + (y - 2)^2 = 4 \\[3ex] \text{Compare to the Standard Form of the equation of a circle: } (x - h)^2 + (y - k)^2 = r^2 \\[3ex] \text{where} \\[3ex] (h, k) = \text{center of the circle} = (2, 2) \\[3ex] h = 2 \\[3ex] k = 2 \\[3ex] r = \text{radius of the circle} = 2 \\[3ex] \text{End point 1} = (x_1 - h, k) = (0, 2)...\text{Given} \\[3ex] (x_1 - 2, 2) = (0, 2) \\[3ex] x_1 - 2 = 0 \\[3ex] x_1 = 0 + 2 \\[3ex] x_1 = 2 \\[3ex] \text{End point 2} = (x_1 + h, k) \\[3ex] = (2 + 2, 2) \\[3ex] = (4, 2) $
$ a.\;\; y = 16x^2 \\[3ex] b.\;\; y = 16 - x^2 \\[3ex] c.\;\; y^2 = 16 - x^2 \\[3ex] d.\;\; y = \dfrac{16}{x} \\[5ex] $
$ a.\;\; y = 16x^2...\text{This is a vertical parabola} \\[5ex] b.\;\; y = 16 - x^2 ...\text{This is a vertical parabola} \\[5ex] c.\;\; y^2 = 16 - x^2 \\[3ex] x^2 + y^2 = 16 ...\text{This is a circle} \\[5ex] d.\;\; y = \dfrac{16}{x} \\[5ex] xy = 16 ...\text{This is a hyperbola whose axis are the asymptotes.} $
$ a.\;\; 5x - 4y = -17 \\[3ex] b.\;\; 5x - 4y = 10 \\[3ex] c.\;\; -2x - 5y = 2 \\[3ex] d.\;\; 5x + 4y = 2 \\[3ex] $
$ 5x - 4y = 2 \\[3ex] 5x - 2 = 4y \\[3ex] 4y = 5x - 2 \\[3ex] y = \dfrac{5x - 2}{4} \\[5ex] y = \dfrac{5}{4}x - \dfrac{2}{4} \\[5ex] y = \dfrac{5}{4}x - \dfrac{1}{2} \\[5ex] \text{Slope, } m = \dfrac{5}{4} \\[5ex] \underline{\text{Equation of the line}} \\[3ex] \text{parallel to }5x - 4y = 2 \implies \text{same slope, } m = \dfrac{5}{4} \\[5ex] \text{passes through } (-2, -5) \\[3ex] x = -2 \\[3ex] y = -5 \\[3ex] y = mx + b ...\text{Slope - Intercept Form} \\[3ex] -5 = \dfrac{5}{4} * -2 + b \\[5ex] -5 = -\dfrac{5}{2} + b \\[5ex] b = -5 + \dfrac{5}{2} \\[5ex] b = \dfrac{-10 + 5}{2} \\[5ex] b = -\dfrac{5}{2} \\[5ex] \implies \\[3ex] y = \dfrac{5}{4}x -\dfrac{5}{2} \\[5ex] \text{LCD} = 4 \\[3ex] 4y = 4 * \dfrac{5}{4}x - 4 * \dfrac{5}{2} \\[5ex] 4y = 5x - 10 \\[3ex] 5x - 4y = 10 $
$ a.\;\; \{x|x \gt 0|\} \\[3ex] b.\;\; \{x|x \lt 0|\} \\[3ex] c.\;\; \{x|x = 1|\} \\[3ex] d.\;\; \{x|x \in W|\} \\[3ex] $
$ -6x - 4 \lt \dfrac{5x + 4}{-1} \\[5ex] -1(-6x - 4) \gt 5x + 4 ...\text{multiplying by a negative number} \\[3ex] 6x + 4 \gt 5x + 4 \\[3ex] 6x - 5x \gt 4 - 4 \\[3ex] x \gt 0 $
$ a.\;\; 15 \\[3ex] b.\;\; \dfrac{5}{3} \\[5ex] c.\;\; 125 \\[3ex] d.\;\; 10 \\[3ex] $
$ \log_5 b = 3 \\[3ex] b = 5^3 ...\text{Relationship Between Exponents and Logarithms} \\[3ex] b = 125 $
a. a negative integer
b. a positive integer
c. a whole number
d. a positive constant
The base should be a positive integer, b > 0
$ a.\;\; -\dfrac{1}{\sqrt{5}} \\[5ex] b.\;\; \dfrac{1}{\sqrt{5}} \\[5ex] c.\;\; \dfrac{1}{2} \\[5ex] d.\;\; \text{cannot be determined} \\[3ex] $
270° ≤ θ ≤ 360° means that θ is in the 4th quadrant
$ \tan\theta = \dfrac{opp}{adj}...\text{SOHCAHTOA} \\[5ex] \tan\theta = -\dfrac{1}{2} \\[5ex] $
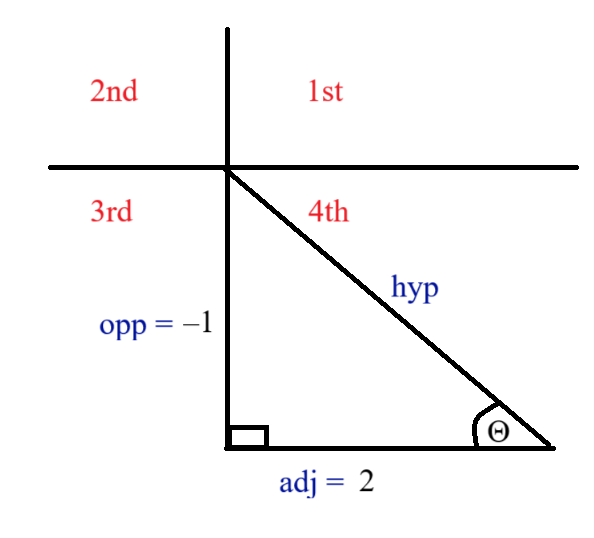
$ hyp^2 = opp^2 + adj^2 ...\text{Pythagorean Theorem} \\[3ex] hyp^2 = (-1)^2 + (-2)^2 \\[3ex] hyp = \sqrt{1 + 4} \\[5ex] hyp = \sqrt{5} \\[5ex] \sin\theta = \dfrac{opp}{hyp}...\text{SOHCAHTOA} \\[5ex] \sin\theta = -\dfrac{1}{\sqrt{5}} $
$ a.\;\; 300 \\[3ex] b.\;\; 60 \\[3ex] c.\;\; 12 \\[3ex] d.\;\; 50 \\[3ex] $
Number of combinations = 3 * 4 * 5 ...Fundamental Counting Principle
= 60 combinations.
How many arrangements would they count in the end?
$ a.\;\; 60 \\[3ex] b.\;\; 24 \\[3ex] c.\;\; 5 \\[3ex] d.\;\; 120 \\[3ex] $
Number of permutations around a circular object (round table) refers to the number of distinct ways people can be arranged when seated around a circular table, where rotations of the same arrangement are considered identical.
$ \text{Number of students, }n = 5 \\[3ex] \text{Number of permutations around a circular object (round table)} \\[3ex] = (n - 1)! \\[3ex] = (5 - 1)! \\[3ex] = 4 * 3 * 2 * 1 \\[3ex] = 24\text{ arrangments} $
$ a.\;\; V(0, 0) \\[3ex] b.\;\; V(0, 3) \\[3ex] c.\;\; V(-3, 0) \\[3ex] d.\;\; V(-3, 3) \\[3ex] $
The y is squared, hence this is a horizontal parabola.
The general form of a horizontal parabola is: $(y - k)^2 = 4p(x - h)$ where:
p the distance from the vertex to the focus and the distance from the vertex to the directrix.
(h, k) is the vertex
$ y^2 = 12x \\[3ex] y^2 = 4 * 3 * x \\[3ex] (y - 0)^2 = 4 * 3 * (x - 0) \\[3ex] \text{Vertex} = (0, 0) $
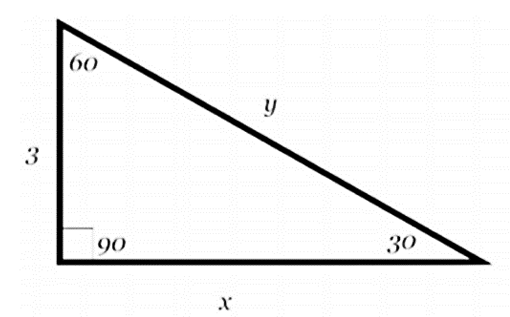
$ a.\;\; \sqrt{3} \\[3ex] b.\;\; 2\sqrt{3} \\[3ex] c.\;\; 6 \\[3ex] d.\;\; 12 \\[3ex] $
$ \sin 30 = \dfrac{3}{y} ...\text{SOHCAHTOA} \\[5ex] \dfrac{1}{2} = \dfrac{3}{y} \\[5ex] \text{Cross Multiply} \\[3ex] y * 1 = 2 * 3 \\[3ex] y = 6 $
$ a.\;\; 1 \\[3ex] b.\;\; 0 \\[3ex] c.\;\; \dfrac{1}{2} \\[5ex] d.\;\; \text{cannot be determined} \\[3ex] $
The derivative of a constant is 0.
What is the sum of a and b?
$ a.\;\; -24 \\[3ex] b.\;\; 32 \\[3ex] c.\;\; -4 \\[3ex] d.\;\; 12 \\[3ex] $
$ 16x - 2y = 48 \\[3ex] 8x - y = 24 \\[3ex] y = 8x - 24 \\[3ex] \text{On the y-axis, } x = 0 \\[3ex] y = 8(0) - 24 \\[3ex] y = 0 - 24 \\[3ex] y = -24 \\[3ex] (x, y) = (a, b) = (0, -24) \\[3ex] a = 0 \\[3ex] b = -24 \\[3ex] a + b = 0 + -24 = -24 $
$ a.\;\; 24 \\[3ex] b.\;\; 18 \\[3ex] c.\;\; 12 \\[3ex] d.\;\; 20 \\[3ex] $
3-digit numbers to be formed from the digits 0, 1, 2, and 3
Restriction:
(1.) No repetition: each digit can be used only once
Given the fact that 012 is the same as 12, we can add another condition:
(2.) The number must not begin with 0
Any of the 3 digits (1, 2, 3) can be the 1st digit: 3 ways
Any of the remaining 2 digits and 0 (3 − 1 + 1 = 3 digits) can be the 2nd digit: 3 ways
Any of the remaining 2 digits (4 − 2 = 2) can be the 3rd digit: 2 ways
$ \text{Number of 3-digit numbers}: \\[3ex] \begin{array}{c c c} \stackrel{\Large 3}{\rule{1cm}{0.5mm}} & \stackrel{\Large 3}{\rule{1cm}{0.5mm}} & \stackrel{\Large 2}{\rule{1cm}{0.5mm}} \end{array} \\[4ex] = 3 * 3 * 2 \\[3ex] = 18\text{ numbers}. $
$ a.\;\; 300 \\[3ex] b.\;\; 297 \\[3ex] c.\;\; 276 \\[3ex] d.\;\; 254 \\[3ex] $
$ 1, 5, 9, 13, ..., 45 \\[3ex] \text{first term, } a = 1 \\[3ex] \text{common difference, } d = 5 - 1 = 4 \\[3ex] \text{last term = nth term, } p = 45 \\[3ex] \text{number of terms, } n = ? \\[3ex] \text{sum of the arithmetic series, } SAS = ? \\[5ex] p = a + d(n - 1) \\[3ex] 45 = 1 + 4(n - 1) \\[3ex] 4(n - 1) = 45 - 1 \\[3ex] n - 1 = \dfrac{44}{4} \\[5ex] n = 11 + 1 \\[3ex] n = 12 \\[5ex] SAS = \dfrac{n(a + p)}{2} \\[5ex] SAS = \dfrac{12(1 + 45)}{2} \\[5ex] = 6(46) \\[3ex] = 276 $
$ a.\;\; (3, 0) \\[3ex] b.\;\; (2, 0) \\[3ex] c.\;\; (1, 0) \\[3ex] d.\;\; (4, 0) \\[3ex] $
$ \text{For the ordered pair: } (-3, 0) \\[3ex] y = 0 \\[3ex] \text{For the parabola: } y = x^2 + 2x - 3 \\[3ex] 0 = x^2 + 2x - 3 \\[3ex] (x + 3)(x - 1) = 0 \\[3ex] x + 3 = 0 \hspace{2em}OR\hspace{2em} x - 1 = 0 \\[3ex] x = -3 \hspace{2em}OR\hspace{2em} x = 1 \\[3ex] x-intercepts = (-3, 0) \text{ and } (1, 0) \\[3ex] (-3, 0)...\text{Given} \\[3ex] \therefore \text{ the other one is } (1, 0) $
$ a.\;\; 8 \\[3ex] b.\;\; -8 \\[3ex] c.\;\; 5 \\[3ex] d.\;\; -5 \\[3ex] $
$ \displaystyle{\lim_{x \to 5}} (3x - 7) \\[3ex] = 3(5) - 7 \\[3ex] = 8 $
Find the value of xy
$ a.\;\; 39 \\[3ex] b.\;\; -2 \\[3ex] c.\;\; 24 \\[3ex] d.\;\; -6 \\[3ex] $
$ x + y = 3...eqn.(1) \\[3ex] x^2 + y^2 = 13...eqn.(2) \\[5ex] (x + y)^2 \\[3ex] = (x + y)(x + y) \\[3ex] = x^2 + xy + xy + y^2 \\[3ex] = x^2 + 2xy + y^2 \\[3ex] = x^2 + y^2 + 2xy \\[3ex] \text{So, } (x + y)^2 = x^2 + y^2 + 2xy \\[3ex] 2xy = (x + y)^2 - (x^2 + y^2) \\[3ex] \text{Substitute for eqn.(1) and eqn.(2)} \\[3ex] 2xy = 3^2 - 13 \\[3ex] 2xy = 9 - 13 \\[3ex] xy = -\dfrac{4}{2} \\[5ex] xy = -2 $
(Answer must be decimal to the nearest hundredth.)
$ a.\;\; 7.69\% \\[3ex] b.\;\; 8.33\% \\[3ex] c.\;\; 7.14\% \\[3ex] d.\;\; 5.88\% \\[3ex] $
$ \text{Mean} = \dfrac{\text{Sum}}{\text{Sample Size}} \\[5ex] \implies \\[3ex] \bar{x} = \dfrac{\Sigma x}{n} \\[5ex] \bar{x} = \dfrac{\Sigma x}{14} \\[5ex] \bar{x} = \dfrac{1}{14} * \Sigma x \\[5ex] \text{Convert } \dfrac{1}{14} \text{ to percent} \\[5ex] \dfrac{1}{14} * 100 \\[5ex] = \dfrac{50}{7} \\[5ex] \approx 7.14\% $
$ a.\;\; _4C_3\\[3ex] b.\;\; \dfrac{_4C_3 * _{52}C_2}{_{52}C_5} \\[5ex] c.\;\; \dfrac{_4C_3 * _{48}C_2}{_{52}C_5} \\[5ex] d.\;\; \dfrac{_{52}C_3}{_{52}C_5} \\[5ex] $
1st: 5 cards must be drawn from 52 cards
Number of ways of drawing 5 cards from 52 cards = $_{52}C_5$
2nd: 3 of the 5 cards must be aces
In a deck of 52 cards, there are 4 aces
So, we need to select 3 of those 4 aces
Number of ways of drawing 3 aces from 4 aces = $_4C_3$
3rd: The remaining 2 cards must be non-aces
The 2 non-aces cards are selected from 48 (52 − 4) non-aces
Number of ways of drawing 2 non-aces from 48 non-aces = $_{48}C_2$
∴ The probability of getting 3 aces out of a deck of 52 cards if 5 cards are to be drawn at a time = $\dfrac{_4C_3 * _{48}C_2}{_{52}C_5}$
$ a.\;\; (\sec\theta)^2\; d\theta \\[3ex] b.\;\; -(\csc\theta)^2\; d\theta \\[3ex] c.\;\; \sec\theta\tan\theta\; d\theta \\[3ex] d.\;\; -\csc\theta\cot\theta\; d\theta \\[3ex] $
Find the value of mn.
$ a.\;\; -\dfrac{1}{2} \\[5ex] b.\;\; -1 \\[3ex] c.\;\; -\dfrac{3}{4} \\[5ex] d.\;\; -\dfrac{1}{4} \\[5ex] $
$ 81^m = 3 \\[3ex] 3^{(4)m} = 3^1 \\[3ex] 3^{4m} = 3^1 \\[3ex] \text{same base; equate exponents} \\[3ex] 4m = 1 \\[3ex] m = \dfrac{1}{4} \\[5ex] m^n = 64 \\[3ex] \left(\dfrac{1}{4}\right)^n = 4^3 \\[5ex] 4^{(-1)n} = 4^3 \\[3ex] \text{same base; equate exponents} \\[3ex] -n = 3 \\[3ex] n = -3 \\[5ex] mn = \dfrac{1}{4} * -3 \\[5ex] = -\dfrac{3}{4} $
$ a.\;\; \dfrac{1}{2} \\[5ex] b.\;\; 2 \\[3ex] c.\;\; 4 \\[3ex] d.\;\; 8 \\[3ex] $
$ \log x + \log 8 = \log 16 \\[3ex] \log{8x} = \log 16 ...Law\;1...Log \\[3ex] \text{same log base; equate terms} \\[3ex] 8x = 16 \\[3ex] x = \dfrac{16}{8} \\[5ex] x = 2 $
This question is incomplete. If you have the complete question, please contact me.
$ a.\;\; -2 \\[3ex] b.\;\; -2 \\[3ex] c.\;\; 0 \\[3ex] d.\;\; \text{does not exist} \\[3ex] $
This question is incomplete. If you have the complete question, please contact me.
$ a.\;\; -35 \\[3ex] b.\;\; y \text{ has no real values} \\[3ex] c.\;\; \sqrt[3]{2x - 6} \\[3ex] d.\;\; -32 \\[3ex] $
$ 4^3 = |2y + 6| \\[3ex] |2y + 6| = 64 \\[3ex] (2y + 6) = 64 \hspace{2em}OR\hspace{2em} -(2y + 6) = 64...\text{Absolute Values} \\[3ex] 2y + 6 = 64 \hspace{2em}OR\hspace{2em} 2y + 6 = -64 \\[3ex] 2y = 64 - 6 \hspace{2em}OR\hspace{2em} 2y = -64 - 6 \\[3ex] 2y = 58 \hspace{2em}OR\hspace{2em} 2y = -70 \\[3ex] y = \dfrac{58}{2} \hspace{2em}OR\hspace{2em} y = -\dfrac{70}{2} \\[5ex] y = 29 \hspace{2em}OR\hspace{2em} y = -35 $
$ a.\;\; \dfrac{\sin\theta}{\cos\theta} \\[5ex] b.\;\; \dfrac{\cos^2\theta}{\sin^2\theta} \\[5ex] c.\;\; 1 \\[3ex] d.\;\; \dfrac{\sin^2\theta}{\cos^2\theta} \\[5ex] $
$ \dfrac{\cot\theta}{\tan\theta} \\[5ex] = \cot\theta \div \tan\theta \\[3ex] = \dfrac{1}{\tan\theta} * \dfrac{1}{\tan\theta} ...\text{Reciprocal Identity} \\[5ex] = \dfrac{\cos\theta}{\sin\theta} * \dfrac{\cos\theta}{\sin\theta} ...\text{Quotient Identity} \\[5ex] = \dfrac{\cos^2\theta}{\sin^2\theta} $
$ a.\;\; y^2 = 4px \\[3ex] b.\;\; y^2 = -4px \\[3ex] c.\;\; x^2 = 4py \\[3ex] d.\;\; x^2 = -4py \\[3ex] $
A parabola is the set of all points equidistant from a fixed point (known as the focus) and a fixed line ( known as the directrix).
This means that the point, say (x, y) is equidistant from the focus and from the directrix.
In other words, the distance from the point to the focus is the distance from the point to the directrix.
$ \text{distance from the point to the focus} \\[3ex] \text{Point, }(x, y) \hspace{3em} \text{Focus, } (0, p) \\[3ex] \text{distance, }d = \sqrt{(x - 0)^2 + (y - p)^2} \\[3ex] d = \sqrt{x^2 + (y - p)^2} \\[5ex] \text{distance from the point to the directrix} \\[3ex] \text{Point, }(x, y) \hspace{3em} \text{Directrix, } y = -p \\[3ex] d = |y - (-p)| \\[3ex] d = |y + p| \\[5ex] d = d \implies \\[3ex] \sqrt{x^2 + (y - p)^2} = |y + p| \\[3ex] x^2 + [(y - p)(y - p)] = (y + p)^2 \\[3ex] x^2 + y^2 - py - py + p^2 = (y + p)(y + p) \\[3ex] x^2 + y^2 + p^2 - 2py = y^2 + py + py + p^2 \\[3ex] x^2 - 2py = 2py \\[3ex] x^2 = 2py + 2py \\[3ex] x^2 = 4py $
$ a.\;\; 106 \\[3ex] b.\;\; 53 \\[3ex] c.\;\; 61 \\[3ex] d.\;\; 125 \\[3ex] $
$ 1, 5, 13, 29, ... \\[3ex] 1, 1 + 4, 5 + 8, 13 + 16, 29 + 32, ... \\[3ex] 1, 1 + 2(2), 5 + 4(2), 13 + 8(2), 29 + 16(2), ... \\[3ex] \text{5th term} = 29 + 32 = 61 \\[3ex] \text{6th term} = 61 + 32(2) \\[3ex] = 61 + 64 \\[3ex] = 125 $
$ a.\;\; -0.5 \\[3ex] b.\;\; 0.5 \\[3ex] c.\;\; 0 \\[3ex] d.\;\; \text{does not exist} \\[3ex] $
$ \displaystyle{\lim_{x \to 1^{-1}}} \sqrt{(1 - x^2)} \\[3ex] \text{Assume } x = 0.9999999 ...\text{approaching 1 from the left} \\[3ex] = \sqrt{(1 - 0.9999999^2)} \\[3ex] = \sqrt{1 - 1}...0.9999999^2 \approx 1 \\[3ex] = \sqrt{0} \\[3ex] = 0 $
If each student can receive at most one award and section Narra is composed of 30 students, how many possible selections are there?
$ a.\;\; 60 \\[3ex] b.\;\; 120 \\[3ex] c.\;\; 27,405 \\[3ex] d.\;\; 657,720 \\[3ex] $
The question did not specify whether the awards are distinct (in which case, it would be Permutation) or identical (in which case, it would be Combination).
So, we shall assume that the awards are identical.
$ C(n, r) = \dfrac{n!}{(n - r)! * r!} \\[5ex] C(30, 4) = \dfrac{30!}{(30 - 4)! * 4!} \\[5ex] = \dfrac{30 * 29 * 28 * 27 * 26!}{26! * 4 * 3 * 2 * 1} \\[5ex] = 15 * 29 * 7 * 9 \\[3ex] = 27,405 \text{ selections} $
$ a.\;\; \sec^2 u + c \\[3ex] b.\;\; -\csc^2 u + c \\[3ex] c.\;\; \ln|\sec u| + c \\[3ex] d.\;\; \ln|\sec u + \tan u| + c \\[3ex] $
$ \displaystyle\int \tan u \;du \\[3ex] = \displaystyle\int \dfrac{\sin u}{\cos u} \; du ...\text{Quotient Identity} \\[5ex] \underline{\text{Integration by Algebraic Substitution}} \\[3ex] \text{Let } p = \cos u \\[3ex] \dfrac{dp}{du} = -\sin u \\[5ex] \dfrac{du}{dp} = -\dfrac{1}{\sin u} \\[5ex] du = -\dfrac{dp}{\sin u} \\[5ex] \implies \\[3ex] = \displaystyle\int \dfrac{\sin u}{p} * -\dfrac{dp}{\sin u} \\[5ex] = -\displaystyle\int \dfrac{1}{p} \; dp \\[5ex] = -\ln |p| + C \\[3ex] = - \ln |\cos u| + C \\[3ex] = \ln |(\cos u)^{-1}| + C ...Law\;5...Log \\[3ex] = \ln \left|\dfrac{1}{\cos u}\right| + C \\[5ex] = \ln |\sec u| + C ...\text{Reciprocal Identity} $
$ a.\;\; \\[3ex] b.\;\; \\[3ex] c.\;\; \\[3ex] d.\;\; \\[3ex] $


